Пример 2.. Пример 3.

Пример 2.

Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.

Квадратичная форма 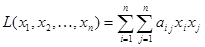называется канонической (или имеет канонический вид), если все ее коэффициенты 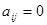при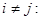

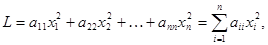
а ее матрица является диагональной.

Справедлива следующая теорема.

Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Пример 3.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.

Теорема (закон инерции квадратичных форм).Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичная форма 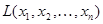называется положительно

(отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

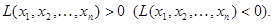
Теорема. Для того чтобы квадратичная форма L = Х'АХ была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 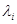матрицы А были положительны (отрицательны).

В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.

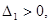
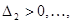
Теорема.Для того чтобы квадратичная форма была положительно определенной, необходимо и недостаточно, чтобы все главные миноры матрицы этой формы были положительны, т.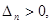е. где

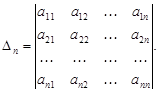
Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака "минус" для минора первого порядка.

Пример 4.

⇐ Предыдущая 12