Хелпикс

Главная

Контакты

Случайная статья



Квадратичные формы. Пример 1.

Стр 1 из 2Следующая ⇒


Квадратичные формы

При решении различных прикладных задач часто приходится исследовать квадратичные формы.

Квадратичной формой 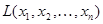от п пере­менных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

 

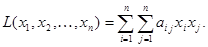                                             (1)

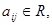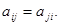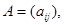
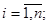
Предполагаем, что коэффициенты квадратичной формы  причем  Матрица  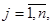составленная из этих коэффициентов, называется матрицей квадратичной формы.

Матрица, у которой все элементы 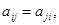 называется симметрической.

Пример: напишите матрицу квадратичной формы: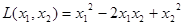

           .

 

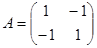В матричной записи квадратичная форма имеет вид:

L = X'AX,                                  (2)

где 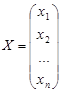    — матрица-столбец переменных.

В самом деле

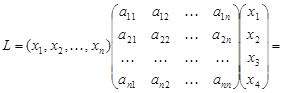
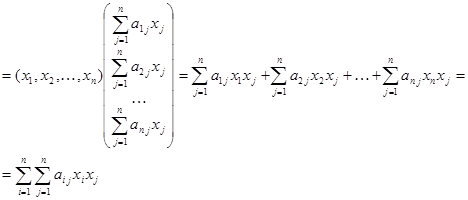и эквивалентность формул (1) и (2) установлена.

 

 

Пример 1.

Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

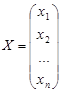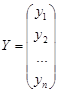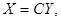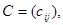
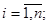
Пусть матрицы-столбцы переменных  и  связаны линейным соотношением  где  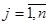есть некоторая невырожденная матрица 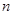-го порядка. Транспонирование произведения матриц проводим по свойству транспонированных матриц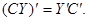

Тогда квадратичная форма

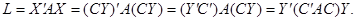
Итак, при невырожденном линейном преобразовании X = CY матрица квадратичной формы принимает вид:

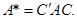                           (3)

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.