
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема (о разложении правильной рациональной дроби на простейшие).
Примеры
1. 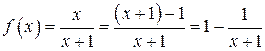
2. 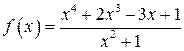 , разделим
, разделим 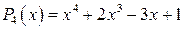 на
на 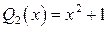 углом, будем иметь
углом, будем иметь

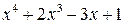
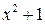


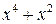
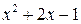
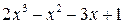

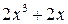
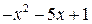

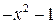
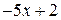
Следовательно, 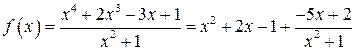 .
.
Пусть дано уравнение 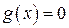 и пусть
и пусть 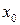 – корень этого уравнения.
– корень этого уравнения.
Говорят, что 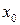 корень кратности k уравнения
корень кратности k уравнения 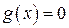 , если
, если
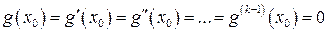 , а
, а 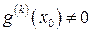 .
.
Пример
Пусть дано уравнение 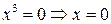 , найдем кратность корня:
, найдем кратность корня:

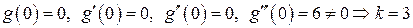
Напомним некоторые сведения из алгебры.
1. Основная теорема алгебры.Всякий многочлен, отличный от постоянной, имеет, по крайней мере, один корень.
2. Если комплексное число 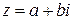 является корнем многочлена с вещественными коэффициентами
является корнем многочлена с вещественными коэффициентами 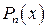 , то и сопряженное ему комплексное число
, то и сопряженное ему комплексное число 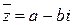 также является корнем многочлена
также является корнем многочлена 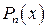 . Если, кроме того, комплексный корень
. Если, кроме того, комплексный корень 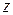 имеет кратность k, то и корень
имеет кратность k, то и корень 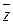 имеет кратность k.
имеет кратность k.
3. Всякий многочлен 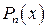 степени n имеет ровно n корней (вещественных и комплексных). Разложение этого многочлена на множители имеет вид:
степени n имеет ровно n корней (вещественных и комплексных). Разложение этого многочлена на множители имеет вид:
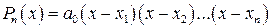 ,
,
где 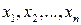 – корни уравнения
– корни уравнения 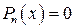 .
.
Если, например, корни 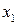 и
и 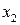 являются комплексно сопряженными, то
являются комплексно сопряженными, то 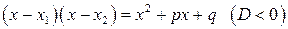 .
.
Итак, всякий многочлен с вещественными коэффициентами разлагается на линейные или квадратичные (с комплексными корнями) множители с вещественными коэффициентами.
4. Теорема (о разложении правильной рациональной дроби на простейшие).
Правильная рациональная дробь вида 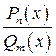 может быть представлена тождественно равной ей суммой простейших рациональных дробей, причем в этой сумме:
может быть представлена тождественно равной ей суммой простейших рациональных дробей, причем в этой сумме:
1) каждому простому вещественному корню а знаменателя 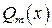 соответствует дробь вида
соответствует дробь вида 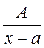 ;
;
2) каждому вещественному корню b кратности k соответствует сумма дробей 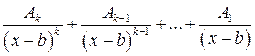 ;
;
3) каждой паре простых комплексно сопряженных корней соответствует дробь вида 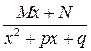 ;
;
4) каждой паре комплексно сопряженных корней кратности k соответствует сумма дробей вида 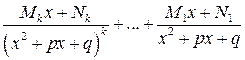 .
.
Пример
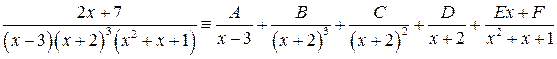
Выводы:
1. Каждому корню знаменателя отвечает столько слагаемых, какова кратность этого корня.
2. Для вещественных корней в числителях дробей – только коэффициенты, а для комплексных – многочлены 1-ой степени.
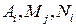 – неопределенные коэффициенты. Для нахождения этих коэффициентов применяются следующие методы:
– неопределенные коэффициенты. Для нахождения этих коэффициентов применяются следующие методы:
1. Метод неопределенных коэффициентов. Согласно этому методу в правой части разложения дроби на простейшие надо привести дроби к общему знаменателю. В результате получим равенство 2-х дробей с одинаковыми знаменателями, а значит, можно приравнять только числители. Приравнивая в числителе коэффициенты при одинаковых степенях х, получим систему уравнений для определения этих коэффициентов.
2. Метод частных значений аргумента. Согласно этому методы в полученное равенство подставляем отдельные значения аргумента, наиболее удобно подставлять вещественные корни знаменателя.
3. Комбинированный метод. Метод состоит в комбинировании двух предыдущих методов. Сначала применяют метод частных значений аргумента (подставляют вещественные корни знаменателя), а затем применяют метод неопределенных коэффициентов.
Пример
Разложить рациональную дробь 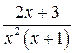 на простейшие.
на простейшие.
Решение.
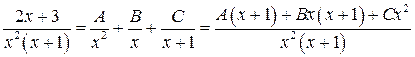
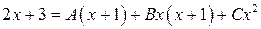 ,
,
применим метод частных значений аргумента:
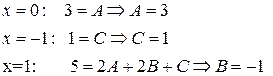 ,
,
применим метод неопределенных коэффициентов:
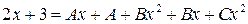
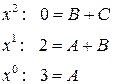 , решив систему уравнений, получаем
, решив систему уравнений, получаем 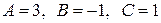 ,
,
Итак, 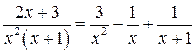 .
.
Вопрос 2. Простейшие дроби и их интегрирование.
Так как любая правильная рациональная дробь представима в виде суммы простейших дробей, то ее интегрирование сводится к интегрированию простейших дробей.
Правильные рациональные дроби вида:
I. 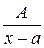 ,
,
II. 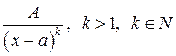 ,
,
III. 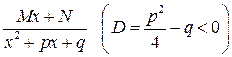 ,
,
IV. 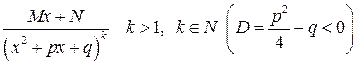 ,
,
где 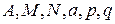 - вещественные числа, называются простейшими рациональными дробями соответственно I, II, III, IY типов.
- вещественные числа, называются простейшими рациональными дробями соответственно I, II, III, IY типов.
Рассмотрим вопрос об интегрировании простейших рациональных дробей первых трех типов.
1. 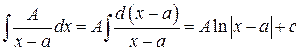
2. 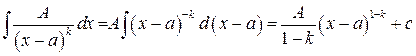
3. 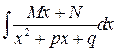 интеграл берется с помощью замены переменной
интеграл берется с помощью замены переменной 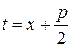 , или методом подведения под знак дифференциала. Этот вопрос был рассмотрен на предыдущей лекции.
, или методом подведения под знак дифференциала. Этот вопрос был рассмотрен на предыдущей лекции.
Пример
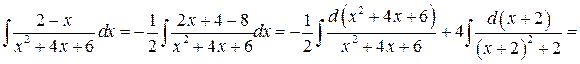
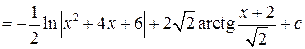
Замечание. Интегрирование рациональных дробей четвертого типа изучить самостоятельно (см. Пискунов Н.С. Дифференциальное и интегральное исчисления, Т.1, гл.10, § 7 стр. 330).
Вопрос 3. Интегрирование рациональных дробей.
Из результатов, полученных при изучении первого и второго вопросов данной лекции, следует теорема.
 Теорема. Неопределенный интеграл от любой рациональной функции всегда существует (на интервалах, в которых знаменатель дроби
Теорема. Неопределенный интеграл от любой рациональной функции всегда существует (на интервалах, в которых знаменатель дроби 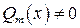 ) и выражается через конечное число элементарных функций, а именно, он является алгебраической суммой, членами которой могут быть лишь многочлены, рациональные дроби, натуральные логарифмы и арктангенсы.
) и выражается через конечное число элементарных функций, а именно, он является алгебраической суммой, членами которой могут быть лишь многочлены, рациональные дроби, натуральные логарифмы и арктангенсы.
Итак, для нахождения неопределенного интеграла от дробно-рациональной функции следует поступать следующим образом:
1) если рациональная дробь неправильная, то делением числителя на знаменатель выделяется целая часть, т.е. данная функция представляется в виде суммы многочлена и правильной рациональной дроби;
2) затем знаменатель полученной правильной дроби разлагается на произведение линейных и квадратичных множителей;
3) эта правильная дробь разлагается на сумму простейших дробей;
4) используя линейность интеграла и формулы, полученные при рассмотрении 2-го вопроса лекции, находятся интегралы от каждого слагаемого в отдельности.
Пример 1
1. 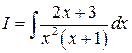
Решение.
Выше было получено, что 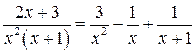 , отсюда имеем
, отсюда имеем
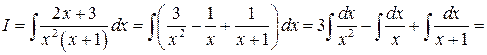
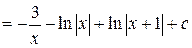 .
.
Пример 2
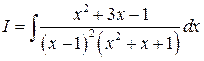
Решение.
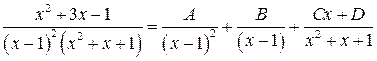
приведя правую часть к общему знаменателю и приравнивая только числители, имеем
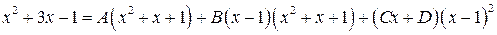
или
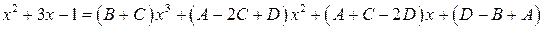
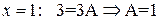
далее применим метод неопределенных коэффициентов:
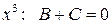
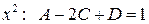 ,
,
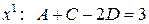
подставив 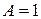 , получим систему уравнений
, получим систему уравнений 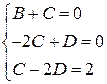 , решая которую находим
, решая которую находим 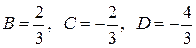 , следовательно, имеем
, следовательно, имеем
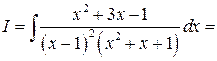
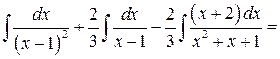
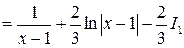
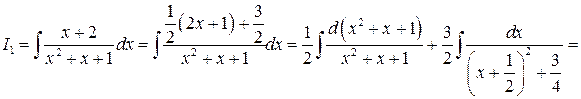
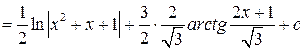 , таким образом, окончательно получаем
, таким образом, окончательно получаем
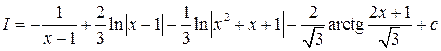
Пример 3
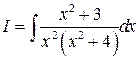
Решение.
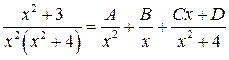 ,
,
после приведения правой части к общему знаменателю, имеем
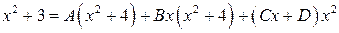
или 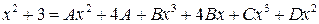 ,
,
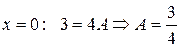 ,
,
Применим теперь метод неопределенных коэффициентов:
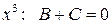
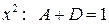 ,
,
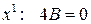
подставляя 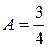 и решая систему, находим
и решая систему, находим 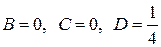 , следовательно, имеем
, следовательно, имеем 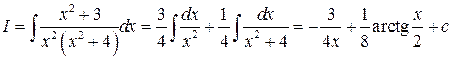 .
.
Выводы.
1. Для нахождения неопределенного интеграла от дробно-рациональной функции следует поступать следующим образом: если рациональная дробь неправильная, то делением числителя на знаменатель выделяется целая часть, т.е. данная функция представляется в виде суммы многочлена и правильной рациональной дроби; затем знаменатель полученной правильной дроби разлагается на произведение линейных и квадратичных множителей; эта правильная дробь разлагается на сумму простейших дробей; затем находятся интегралы от каждого слагаемого в отдельности.
2. Коэффициенты разложения на простейшие дроби можно находить методом неопределенных коэффициентов, методом частных значений аргумента или комбинированным методом.
3. Неопределенный интеграл от любой рациональной функции всегда существует (на интервалах, в которых знаменатель дроби 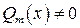 ) и выражается через конечное число элементарных функций, а именно, он является алгебраической суммой, членами которой могут быть лишь многочлены, рациональные дроби, натуральные логарифмы и арктангенсы.
) и выражается через конечное число элементарных функций, а именно, он является алгебраической суммой, членами которой могут быть лишь многочлены, рациональные дроби, натуральные логарифмы и арктангенсы.
Текст лекции разработал:
доцент кафедры №1 Пушкина В.П.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|