ЛЕКЦИЯ № 21. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

ЛЕКЦИЯ № 21

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

по дисциплине Математика

Раздел 3. Интегральное исчисление функции одной переменной

Тема 7. Неопределенный интеграл

Учебная цель: формировать знания о разложении правильной рациональной дроби на простейшие, об интегрировании рациональных дробей.

Учебные вопросы:

1. Разложение правильной рациональной дроби на простейшие. Нахождение неизвестных коэффициентов.

2. Простейшие дроби и их интегрирование.

3. Интегрирование рациональных дробей.

Литература:

1. Высшая математика для экономистов : учебник / под ред. Н. Ш. Кремера. – М. : ЮНИТИ, 2006.

2. Письменный, Д. Т. Конспект лекций по высшей математике : в 2 ч. Ч. 1 / Д. Т. Письменный. - М. : Айрис-пресс, 2003.

Санкт – Петербург

Вопрос 1. Разложение правильной рациональной дроби на простейшие.

Нахождение неизвестных коэффициентов.

Рассмотрим функцию вида

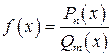, ( 1 )

где 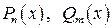- многочлены степени n и m соответственно

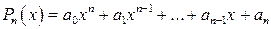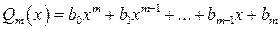Функция вида (1) называется рациональной функцией или рациональной дробью.

Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе, т.е. .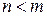

Если 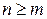, то рациональная дробь называется неправильной.

Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби, т.е.

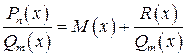, ( 2 )

где 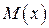– многочлен степени 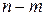, 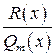– правильная рациональная дробь, 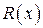– остаток – многочлен степени меньше т. Это представление единственно.

Интегрирование многочлена 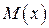не представляет труда, весь вопрос заключается в интегрировании правильных рациональных дробей.

Выделение целой части (многочлена 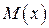) производится с помощью преобразования числителя дроби (в простых случаях) или, в общем случае, делением многочле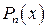на на 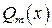углом.

12 Следующая ⇒