
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа №2
7.3. Контрольная работа №2
Дифференциальное исчисление функций нескольких переменных
Задание 1. Дана функция z=z(x; y), точкаА(x0; y0) и вектор а. Найти производную в точке А в направление вектора ā.
1.1. 
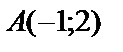
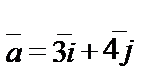 .
.
1) 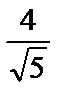 ; 2)
; 2) 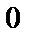 ; 3)
; 3) 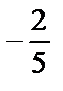 ; 4)
; 4) 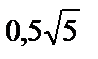 ; 5)
; 5) 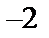 .
.
1.2. 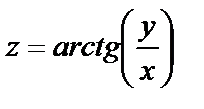
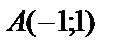
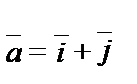 .
.
1) 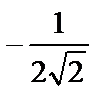 ; 2)
; 2) 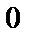 ; 3)
; 3) 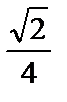 ; 4)
; 4) 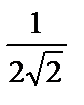 ; 5)
; 5)  .
.
1.3. 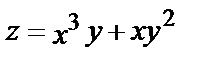
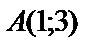
 .
.
1) 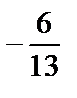 ; 2)
; 2) 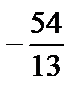 ; 3)
; 3) 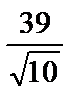 ; 4)
; 4) 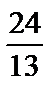 ; 5)
; 5) 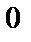 .
.
1.4. 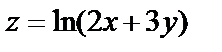
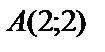
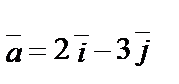 .
.
1) 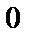 ; 2)
; 2) 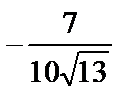 ; 3)
; 3) 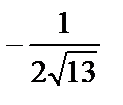 ; 4)
; 4) 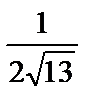 ; 5)
; 5) 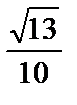 .
.
1.5. 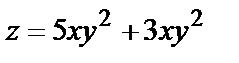

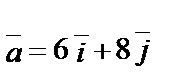 .
.
1) 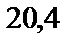 ; 2)
; 2) 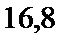 ; 3)
; 3)  ; 4)
; 4) 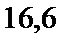 ; 5)
; 5) 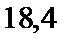 .
.
1.6. 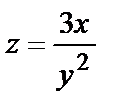
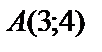
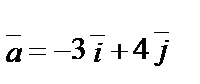 .
.
1) 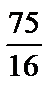 ; 2)
; 2) 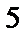 ; 3)
; 3) 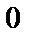 ; 4)
; 4) 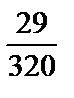 ; 5)
; 5)  .
.
1.7. 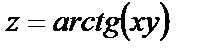
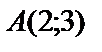
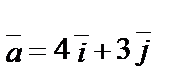 .
.
1) 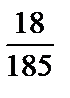 ; 2)
; 2) 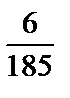 ; 3)
; 3) 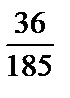 ; 4)
; 4) 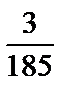 ; 5)
; 5) 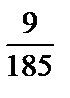 .
.
1.8. 
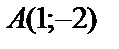
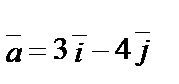 .
.
1) 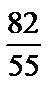 ; 2)
; 2) 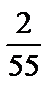 ; 3)
; 3) 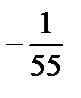 ; 4)
; 4) 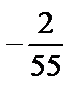 ; 5)
; 5) 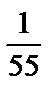 .
.
1.9. 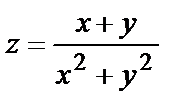
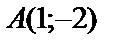
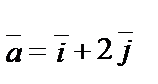 .
.
1) 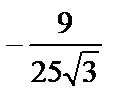 ; 2)
; 2) 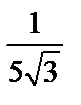 ; 3)
; 3) 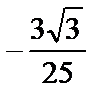 ; 4)
; 4) 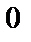 ; 5)
; 5) 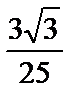 .
.
1.10. 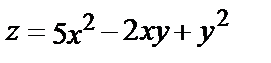
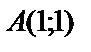
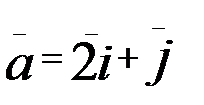 .
.
1) 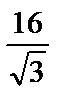 ; 2)
; 2) 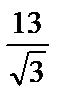 ; 3)
; 3) 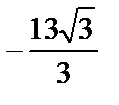 ; 4)
; 4) 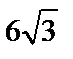 ; 5)
; 5)  .
.
1.11. z=x2+xy+y2 A(1;1), 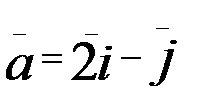 .
.
1.12. z=2x2+3xy+y2 A(2;1), 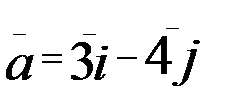 .
.
1.13. z=In(5x2+3y2); A(1;1), 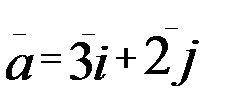 .
.
1.14. z=In(5x2+4y2); A(1;1), 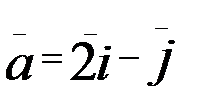 .
.
1.15. z=5x2+6xy; A(2;1), 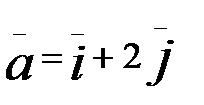 .
.
Задание 2.
Вычислите следующие интегралы:
2.1.1. 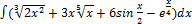 2.1.9.
2.1.9. 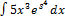
2.1.2. 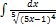 2.1.10.
2.1.10. 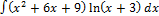
2.1.3. 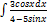 2.1.11.
2.1.11. 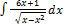
2.1.4. 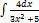 2.1.12.
2.1.12. 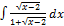
2.1.5. 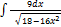 2.1.13.
2.1.13. 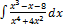
2.1.6. 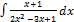 2.1.14.
2.1.14. 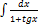
2.1.7. 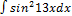 2.1.15.
2.1.15. 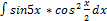
2.1.8. 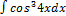
Вычислите следующие интегралы:
2.2.1. 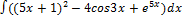 2.2.9.
2.2.9. 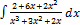
2.2.2. 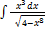 2.2.10.
2.2.10. 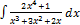
2.2.3. 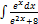 2.2.11.
2.2.11. 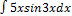
2.2.4. 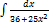 2.2.12.
2.2.12. 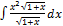
2.2.5.  2.2.13.
2.2.13. 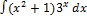
2.2.6. 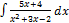 2.2.14.
2.2.14. 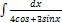
2.2.7. 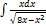 2.2.15.
2.2.15. 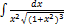
2.2.8. 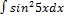
Вычислите следующие интегралы:
2.3.1. 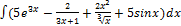 2.3.9.
2.3.9. 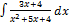
2.3.2. 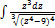 2.3.10.
2.3.10. 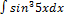
2.3.3. 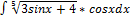 2.3.11.
2.3.11. 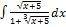
2.3.4. 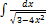 2.3.12.
2.3.12. 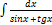
2.3.5. 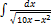 2.3.13.
2.3.13. 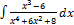
2.3.6. 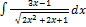 2.3.14.
2.3.14. 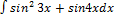
2.3.7. 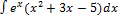 . 2.3.15.
. 2.3.15. 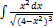
2.3.8. 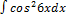
Вычислите следующие интегралы:
2.4.1. 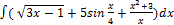 2.4.9.
2.4.9. 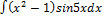
2.4.2. 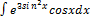 2.4.10.
2.4.10. 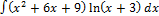
2.4.3. 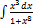 2.4.11.
2.4.11. 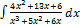
2.4.4. 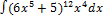 2.4.12.
2.4.12. 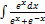
2.4.5. 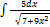 2.4.13.
2.4.13. 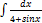
2.4.6. 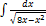 2.4.14.
2.4.14. 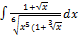
2.4.7.  2.4.15.
2.4.15. 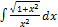
2.4.8. 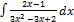
Вычислите следующие интегралы:
2.5.1. 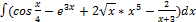 2.5.9.
2.5.9. 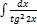
2.5.2. 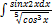 2.5.10.
2.5.10. 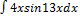
2.5.3. 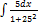 2.5.11.
2.5.11. 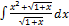
2.5.4. 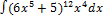 2.5.12.
2.5.12. 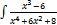 dx
dx
2.5.5. 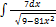 2.5.13.
2.5.13. 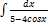
2.5.6. 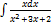 2.5.14.
2.5.14. 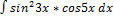
2.5.7. 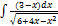 2.5.15.
2.5.15. 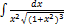
2.5.8. 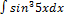
Вычислите следующие интегралы:
2.6.1. 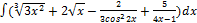 2.6. 9.
2.6. 9. 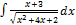
2.6.2. 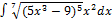 2.6. 10.
2.6. 10. 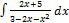
2.6.3. 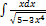 2.6.11.
2.6.11. 
2.6.4. 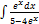 2.6. 12.
2.6. 12. 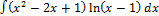
2.6.5. 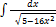 2.6.13.
2.6.13. 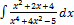
2.6.6. 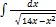 2.6. 14.
2.6. 14. 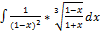
2.6.7. 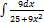 2.6. 15.
2.6. 15. 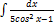
2.6.8. 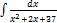
Вычислите следующие интегралы:
2.7.1. 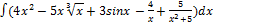 2.7. 9.
2.7. 9. 
2.7.2.  2.7.10.
2.7.10. 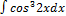
2.7.3.  2.7.11.
2.7.11. 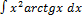
2.7.4.  2.7.12.
2.7.12. 
2.7.5.  2.7.13.
2.7.13. 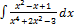
2.7.6.  2.7.14.
2.7.14. 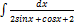
2.7.7.  2.7.15.
2.7.15. 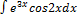
2.7.8. 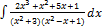
Вычислите следующие интегралы:
2.8.1. 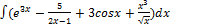 2.8.9.
2.8.9. 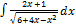
2.8.2.  2.8.10.
2.8.10. 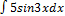
2.8.3.  2.8.11.
2.8.11. 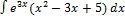
2.8.4.  2.8.12.
2.8.12. 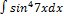
2.8.5.  2.8.13.
2.8.13. 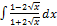
2.8.6.  2.8.14.
2.8.14. 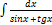
2.8.7.  2.8.15.
2.8.15. 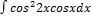
2.8.8. 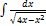
Вычислите следующие интегралы:
2.9.1. 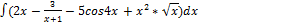 2.9. 9.
2.9. 9. 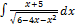
2.9.2.  2.9.10.
2.9.10. 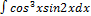
2.9.3.  2.9.11.
2.9.11. 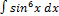
2.9.4.  2.9.12.
2.9.12. 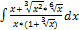
2.9.5. 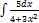 2.9.13.
2.9.13. 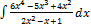
2.9.6.  2.9.14.
2.9.14. 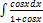
2.9.7.  2.9.15.
2.9.15. 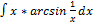
2.9.8. 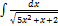
Вычислите следующие интегралы:
2.10.1. 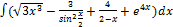 2.10.9.
2.10.9. 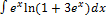
2.10.2.  2.10.10.
2.10.10. 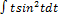
2.10.3.  2.10.11.
2.10.11. 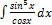
2.10.4.  2.10.12.
2.10.12. 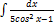
2.10.5. 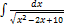 2.10.13.
2.10.13. 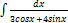
2.10.6.  2.10.14.
2.10.14. 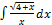
2.10.7. 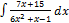 2.10.15.
2.10.15. 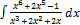
2.10.8. 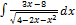
Вычислите следующие интегралы:
2.11.1. 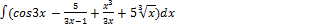 2.11.9.
2.11.9. 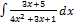
2.11.2. 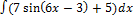 2.11.10.
2.11.10. 
2.11.3. 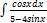 2.11.11.
2.11.11. 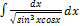
2.11.4.  2.11.12.
2.11.12. 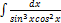
2.11.5.  2.11.13.
2.11.13. 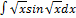
2.11.6.  2.11. 14.
2.11. 14. 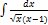
2.11.7.  2.11.15.
2.11.15. 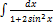
2.11.8. 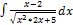
Вычислите следующие интегралы:
2.12.1. 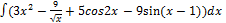 2.12.9.
2.12.9. 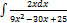
2.12.2. 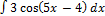 2.12.10.
2.12.10. 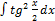
2.12.3. 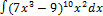 2.12.11.
2.12.11. 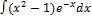
2.12.4.  2.12.12.
2.12.12. 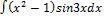
2.12.5. 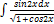 2.12.13.
2.12.13. 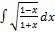
2.12.6.  2.12.14.
2.12.14. 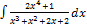
2.12.7.  2.12. 15.
2.12. 15. 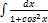
2.12.8. 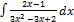
Вычислите следующие интегралы:
2.13.1. 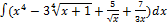 2.13. 9.
2.13. 9. 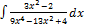
2.13.2. 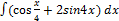 2.13.10.
2.13.10. 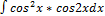
2.13.3. 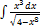 2.13.11.
2.13.11. 
2.13.4. 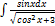 2.13.12.
2.13.12. 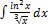
2.13.5. 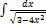 2.13.13.
2.13.13. 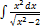
2.13.6.  2.13.14.
2.13.14. 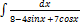
2.13.7. 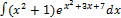 2.13.15.
2.13.15. 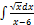
2.13.8. 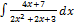
Вычислите следующие интегралы:
2.14.1. 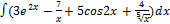 2.14.9.
2.14.9. 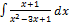
2.14.2. 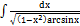 2.14.10.
2.14.10. 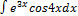
2.14.3. 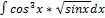 2.14.11.
2.14.11. 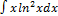
2.14.4. 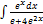 2.14.12.
2.14.12. 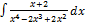
2.14.5. 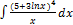 2.14.13.
2.14.13. 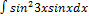
2.14.6.  2.14. 14.
2.14. 14. 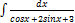
2.14.7.  2.14.15.
2.14.15. 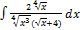
2.14.8. 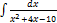
Вычислите следующие интегралы:
2.15.1. 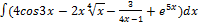 2.15. 9.
2.15. 9. 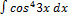
2.15.2. 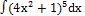 2.15.10.
2.15.10. 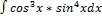
2.15.3. 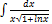 2.15.11.
2.15.11. 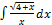
2.15.4. 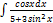 2.15.12.
2.15.12. 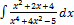
2.15.5. 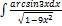 2.15.13.
2.15.13. 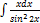
2.15.6.  2.15.14.
2.15.14. 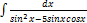
2.15.7. 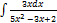 2.15.15.
2.15.15. 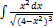
2.15.8. 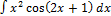
Задание 3. Вычислить (внесение функции под знак дифференциала).
3.1. 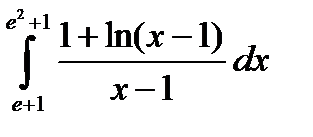
3.2. 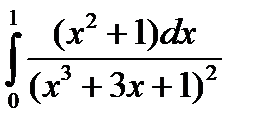
3.3. 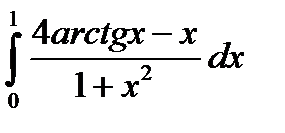
3.4. 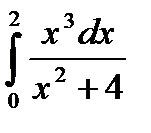
3.5. 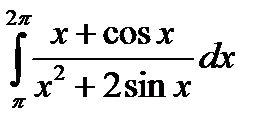
3.6. 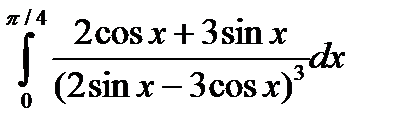
3.7. 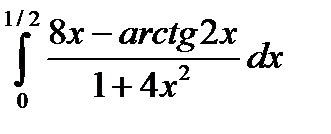
3.8. 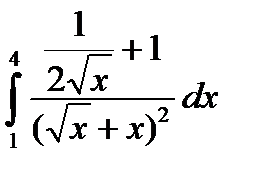
3.9. 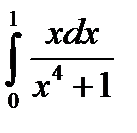
3.10. 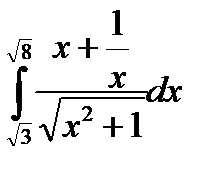
3.11. 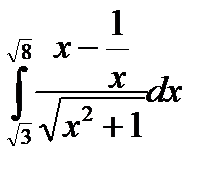
3.12. 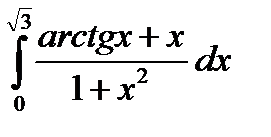
3.13. 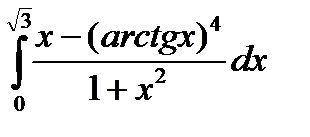
3.14. 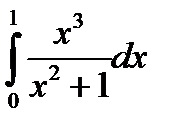
3.15. 
Задание 4.Вычислить применением метода интегрирования по частям.
4.1. 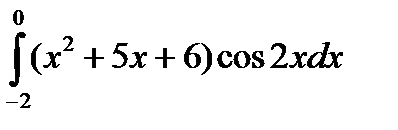
4.2. 
4.3. 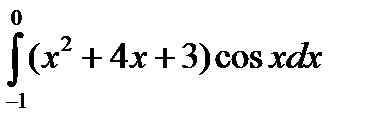
4.4. 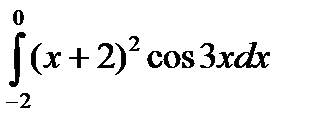
4.5. 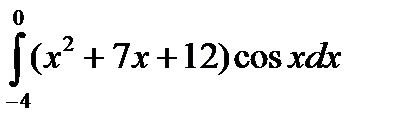
4.6. 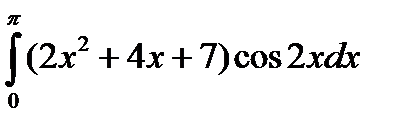
4.7. 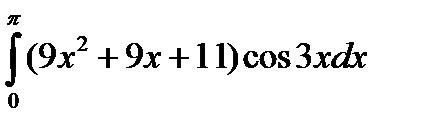
4.8. 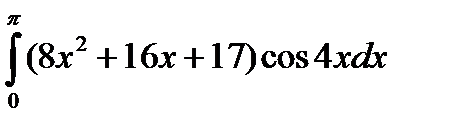
4.9. 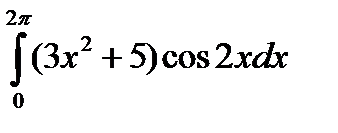
4.10. 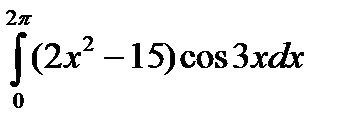
4.11. 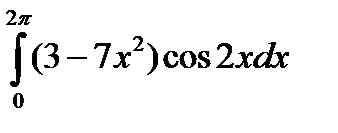
4.12. 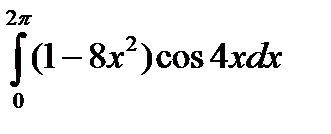
4.13. 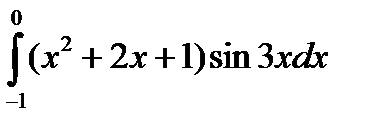
4.14. 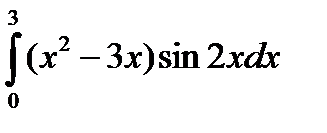
4.15. 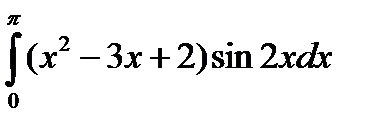
Задание 5. Вычислить универсальной подстановкой.
5.1. 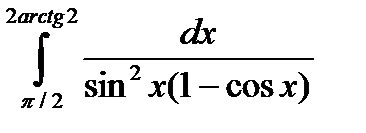
5.2. 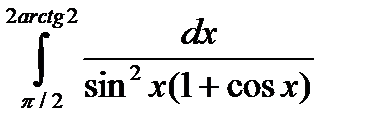
5.3. 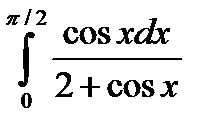
5.4. 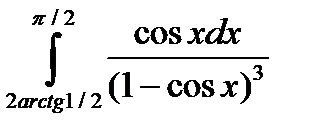
5.5. 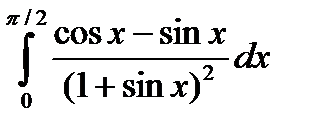
5.6. 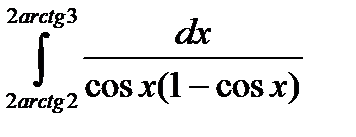
5.7. 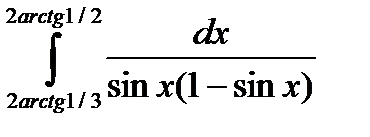
5.8. 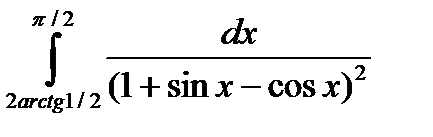
5.9 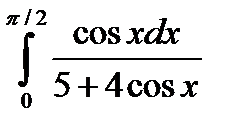
5.10. 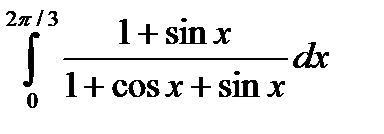
5.11. 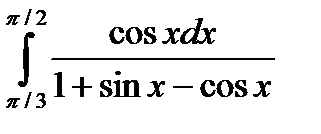
5.12. 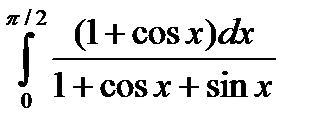
5.13. 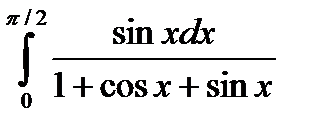
5.14. 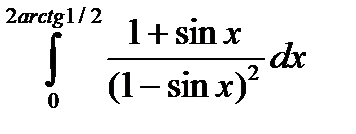
5.15. 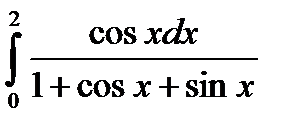
Задание 6.
Вычислить площадь плоской фигуры.
6.1Вычислить площадь фигуры, ограниченной кривой 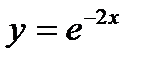 , прямыми х=-0,5, х=1 и осью абсцисс.
, прямыми х=-0,5, х=1 и осью абсцисс.
6.2Найти площадь фигуры, ограниченной кривой 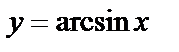 , прямыми
, прямыми 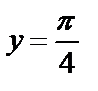 ,
, 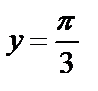 и осью ординат.
и осью ординат.
6.3Найти площадь фигуры, заключенной между окружностью 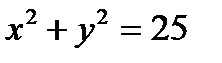 и прямыми 2у-5=0,
и прямыми 2у-5=0, 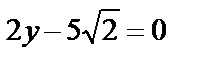
6.4Найти площадь фигуры, ограниченной эллипсом 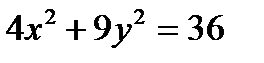 , прямой
, прямой 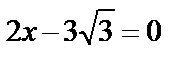 и осью ординат.
и осью ординат.
6.5Найти площадь фигуры, ограниченной ветвью гиперболы 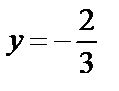 и прямыми х=1; х=5.
и прямыми х=1; х=5.
6.6Вычислить площадь фигуры, ограниченной кривой 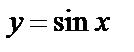 и осью абсцисс от
и осью абсцисс от 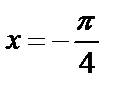 до
до 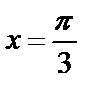 .
.
6.7 Найти площадь фигуры, ограниченной кривой 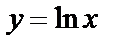 , прямыми
, прямыми 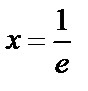 , х=е и осью абсцисс.
, х=е и осью абсцисс.
6.8 Вычислить площадь фигуры, ограниченной параболой 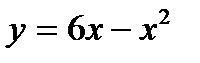 , прямыми х=-1, х=3 и осью абсцисс.
, прямыми х=-1, х=3 и осью абсцисс.
6.9 Найти площадь фигуры, ограниченной параболой 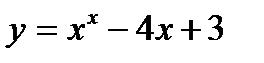 , осями координат и прямой х=4.
, осями координат и прямой х=4.
6.10 Найти площадь фигуры, заключенной между прямыми у=2х, у=5х, х=2, х=6.
6.11 Найти площадь части гиперболы  , отсекаемой от нее прямой х+у-4=0.
, отсекаемой от нее прямой х+у-4=0.
6.12 Найти площадь фигуры, отсекаемой от параболы 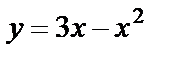 прямой 5х-у-8=0.
прямой 5х-у-8=0.
6.13 Вычислить площадь фигуры, ограниченной параболой 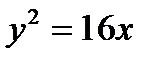 и прямой у=х.
и прямой у=х.
6.14 Найти площадь фигуры, заключенной между параболами 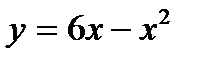 и
и 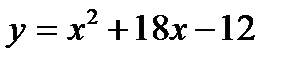 .
.
6.15 Вычислить площадь фигуры, заключенной между параболами 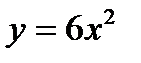 и
и 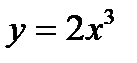 .
.
Задание 7.
Вычислить длину дуги.
7.1. y2 = x3 от х=0 до х=5
7.2. y=lnsinx от х= 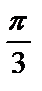 до х=
до х= 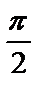
7.3. 2у= x2 -3 между точками пересечения с осью Ox
7.4. x= 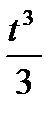 - t, y=t2+2 от t=1 до t=4
- t, y=t2+2 от t=1 до t=4
7.5. x=4(t-sint), y=4(1-cost) (длину дуги одной арки циклоиды)
7.6. 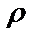 =5sin
=5sin 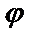
7.7. 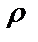 =sin3
=sin3 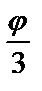 от
от 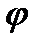 =0 до
=0 до 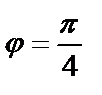
7.8. y=lnx от х= 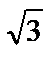 до x=2
до x=2 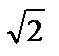
7.9. x= 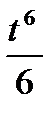 , y=2-
, y=2- 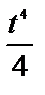 (между точками пересечения с координатными осями)
(между точками пересечения с координатными осями)
7.10. 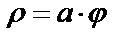 (длину первого витка спирали Архимеда)
(длину первого витка спирали Архимеда)
7.11. x= 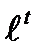 cost, y=
cost, y= 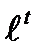 sint от t=0 до t=ln
sint от t=0 до t=ln 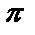
7.12. 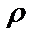 =1-cos
=1-cos 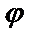
7.13. 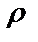 =2sin
=2sin 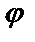
7.14. 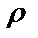 =2sin3
=2sin3 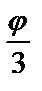
7.15. x 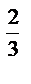 +y
+y 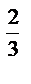 =9
=9
Задание 8.
8.1. Вычислить объём тела, образованного вращением вокруг оси фигуры, ограниченной дугой кубической параболы y=x3-4x и осью абсцисс.
8.2. Определить объём тела, полученного в результате вращения вокруг оси ОХ фигуры, которая ограничена дугой окружности х2+y2=16, лежащей в I четверти, и прямыми х=1 и х=3.
8.3. Найти объём тела, образованного вращением эллипса 4x2+9y2=36 вокруг малой оси.
8.4. Фигура, ограниченная дугой эллипса 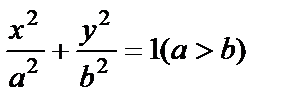 и двумя прямыми, перпендикулярными к оси абсцисс и проходящими через фокусы эллипса, вращается вокруг оси ОХ. Определить объём тела вращения.
и двумя прямыми, перпендикулярными к оси абсцисс и проходящими через фокусы эллипса, вращается вокруг оси ОХ. Определить объём тела вращения.
8.5. Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной ветвью гиперболы x2-y2=1 и прямой х=3.
8.6. Найти объем тела, образованного вращением астероиды x=acos3t, y=asin3t вокруг оси ОХ.
8.7. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной одной аркой циклоиды х=a(t-sint), y=a(1-cost) и отрезком 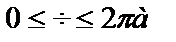 оси абсцисс.
оси абсцисс.
8.8. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами y=2x2 и y=x3.
8.9. Фигура, образованная в результате пересечения параболы y2=4x и прямой y=x, вращается вокруг оси Ох. Найти объём тела вращения.
8.10. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой y2=2x и прямой 2х+2у-3=0.
8.11. Вычислить объем тела, образованного вращением общей части парабол y=x2 и y2=8x: а)вокруг оси Ох; б)вокруг оси Оу.
8.12. Фигура, ограниченная кривыми y=tgx, y=ctgx и прямой x= 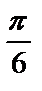 , вращается вокруг оси OX. Найти объем тела вращения.
, вращается вокруг оси OX. Найти объем тела вращения.
8.13. Найти объем тела, полученного в результате вращения вокруг оси OX сегмента, отсекаемого прямой х+у-2=0 от круга, граничная окружность которого x2+y2=4
8.14. Определить объем тела, образованного вращением вокруг оси ОY фигуры, ограниченной кривыми y=log2x, y=log4x и прямой y=1.
8.15. Фигура, лежащая в I четверти и ограниченная дугой окружности x2+y2=18, параболой 3y=x2 и осью ординат, вращается вокруг оси Ох. Найти объем тела вращения.
Задание 9.
Вычислить несобственный интеграл (исследовать его сходимость).
9.1. 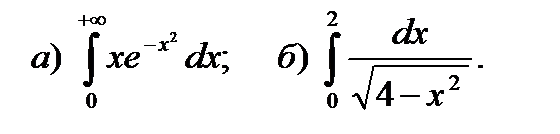
9.2. 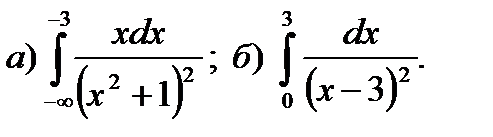
9.3. 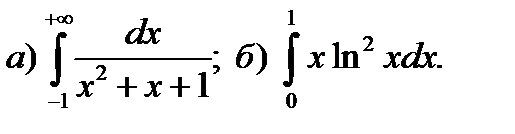
9.4. 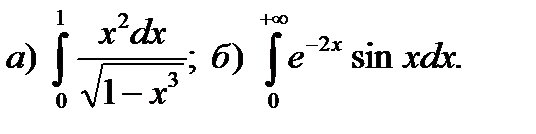
9.5. 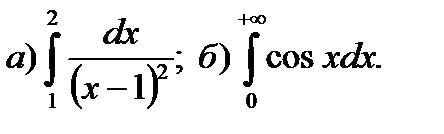
9.6. 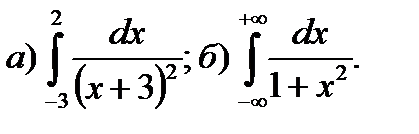
9.7. 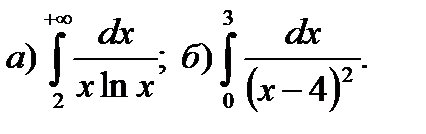
9.8. 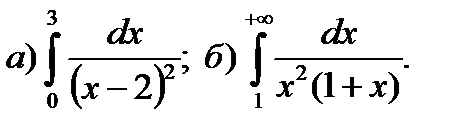
9.9. 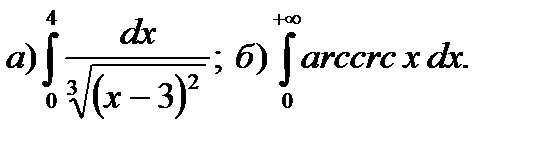
9.10. 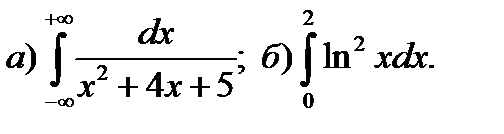
9.11. 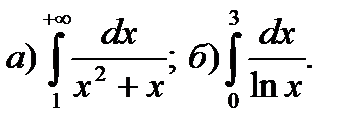
9.12. 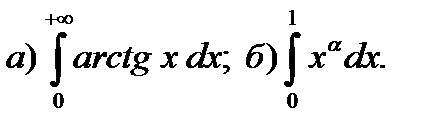
9.13. 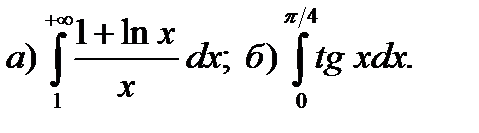
9.14. 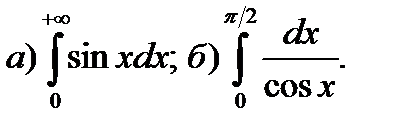
9.15. 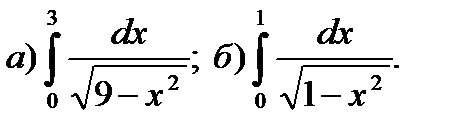
Задание 10.
Изменить порядок интегрирования. Область интегрирования изобразить на чертеже.
10.1. 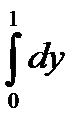
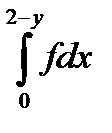 10.2.
10.2. 
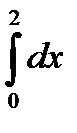
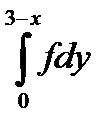
10.3. 
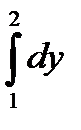
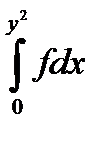 10.4.
10.4. 
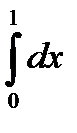
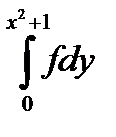
10.5. 
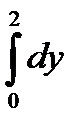
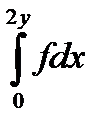 10.6.
10.6. 
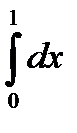
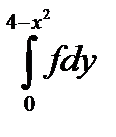
10.7. 
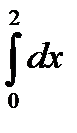
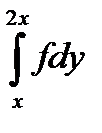 10.8.
10.8. 
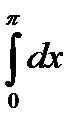
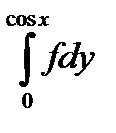
10.9. 
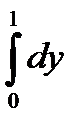
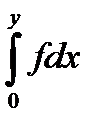 10.10.
10.10. 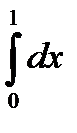
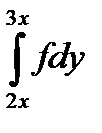
10.11. 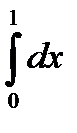
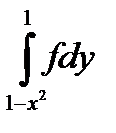 +
+ 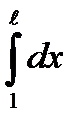
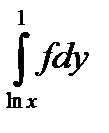
10.12. 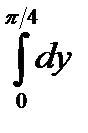
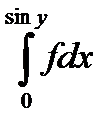 +
+ 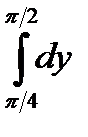
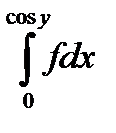
10.13. 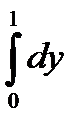
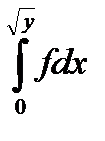 +
+ 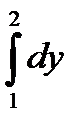
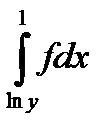
10.14. 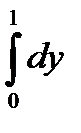
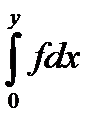 +
+ 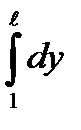
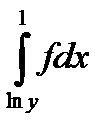
10.15. 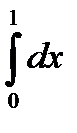
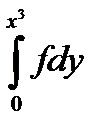 +
+ 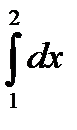
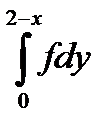
Задание 11.
Вычислить:
11.1. 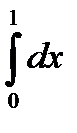
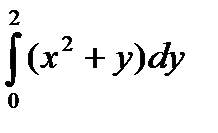 11.2.
11.2. 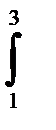
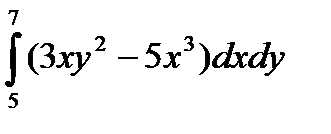
11.3. 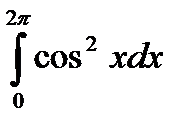
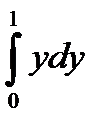 11.4.
11.4. 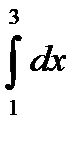
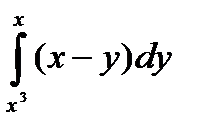
11.5. 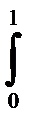
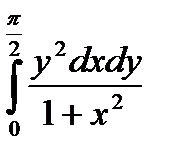
 11.6.
11.6. 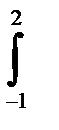
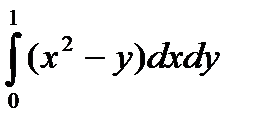
11.7. 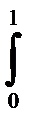
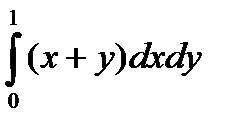 11.8.
11.8. 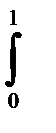
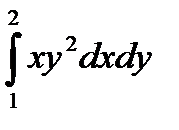
11.9. 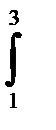
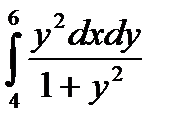 11.10.
11.10. 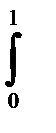
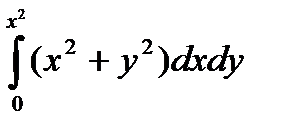
11.11. 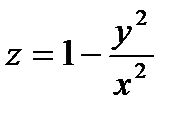 , D:
, D: 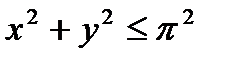
11.12. 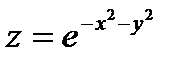 , D:
, D: 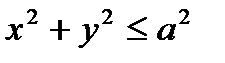
11.13. 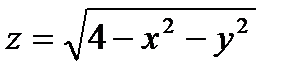 , D:
, D: 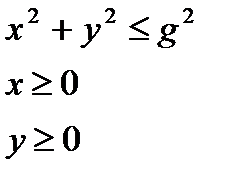
11.14. 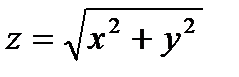 , D:
, D: 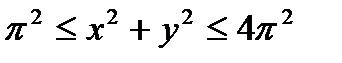
11.15. 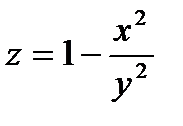 , D:
, D: 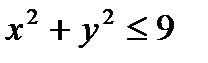
Задание 12.
Найти площадь фигуры, ограниченной линиями:
12.1. 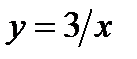 ,
, 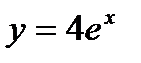 ,
, 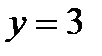 ,
, 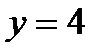 .
.
12.2. 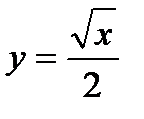 ,
, 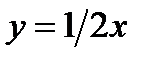 ,
, 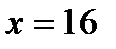 ,
, 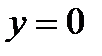 .
.
12.3. 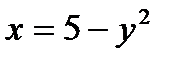 ,
, 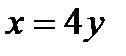 ,
, 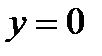 .
.
12.4. 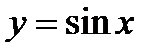 ,
, 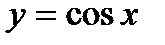 ,
, 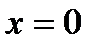 (
( 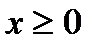 ),
), 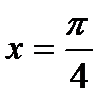 .
.
12.5. 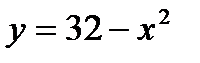 ,
,  .
.
12.6. 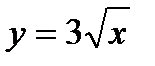 ,
, 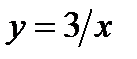 ,
, 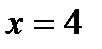 .
.
12.7. 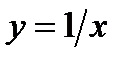 ,
, 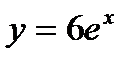 ,
, 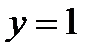 ,
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};
,
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|