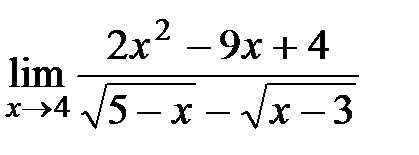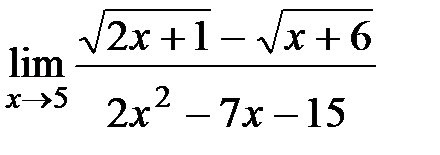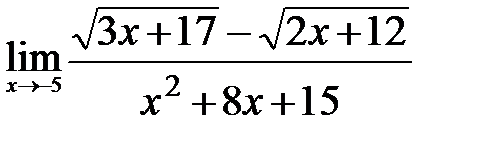- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольные работы для заочников 1 курса (1 семестр)
Контрольные работы для заочников 1 курса (1 семестр)
Контрольная работа №1
Задание 1. Для матрицы третьего порядка вычислите ее определитель
и определитель матрицы, транспонированной к данной.
1. 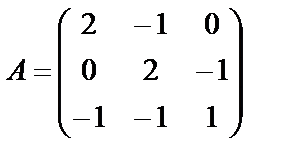 ; 2.
; 2. 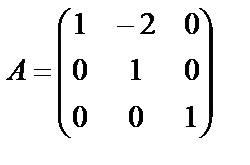 ; 3.
; 3. 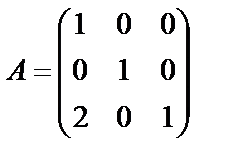 ;
;
4. 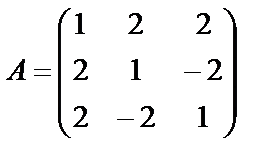 ; 5.
; 5. 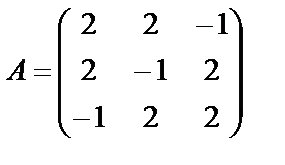 ; 6.
; 6. 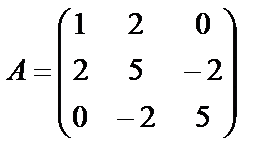 ;
;
7. 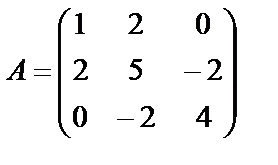 ; 8.
; 8. 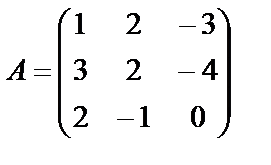 ; 9.
; 9. 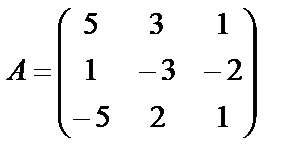 ;
;
10. 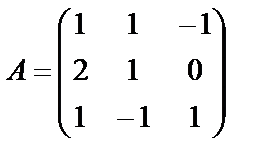 ; 11.
; 11. 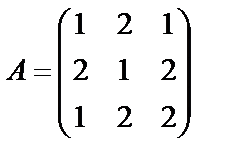 ; 12.
; 12. 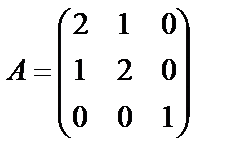 ;
;
13. 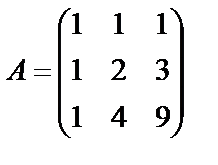 ; 14.
; 14. 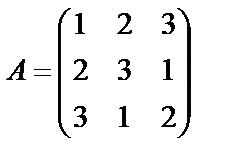 ; 15.
; 15. 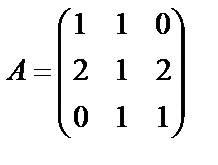 ;
;
16. 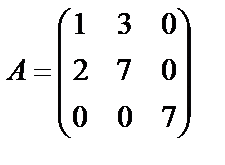 ; 17.
; 17. 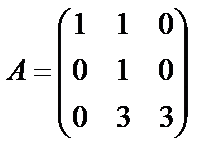 ; 18.
; 18. 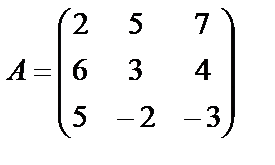 ;
;
19. 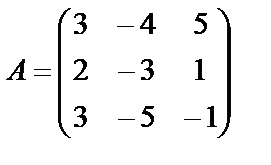 ; 20.
; 20. 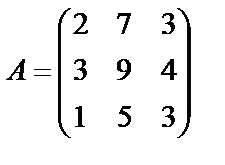
Задание 2. Решите систему линейных уравнений матричным способом и проверить вторым способом методом Гаусса.
1. 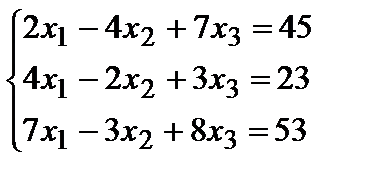 ; 2.
; 2. 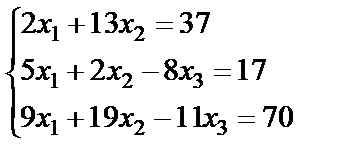 ;
;
3. 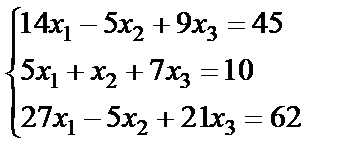 ; 4.
; 4. 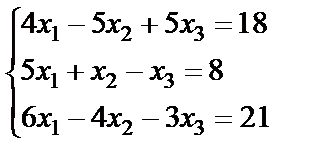 ;
;
5. 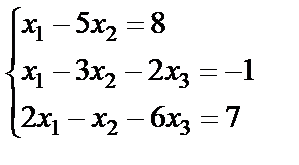 ; 6.
; 6. 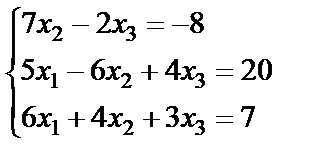 ;
;
7. 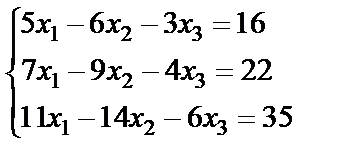 ; 8.
; 8. 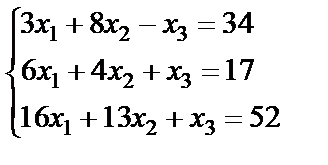 ;
;
9. 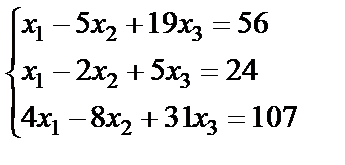 ; 10.
; 10. 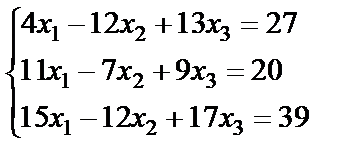 ;
;
11. 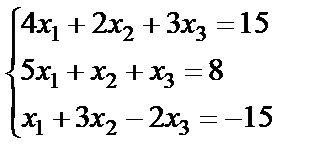 ; 12.
; 12. 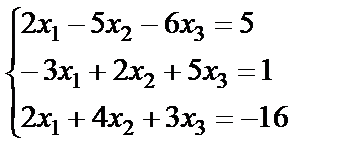 ;
;
13. 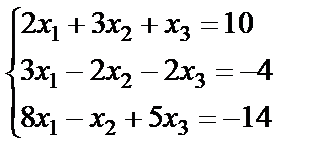 ; 14.
; 14. 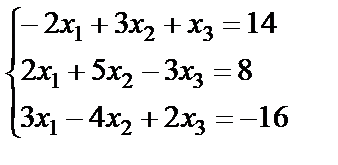 ;
;
15. 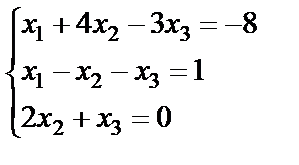 ; 16.
; 16. 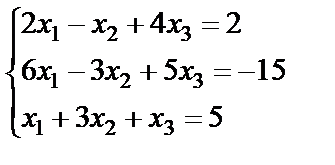 ;
;
17. 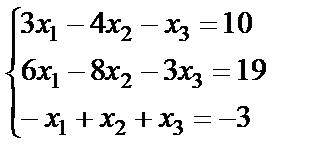 ; 18.
; 18. 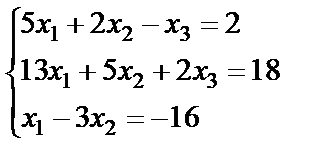 ;
;
19. 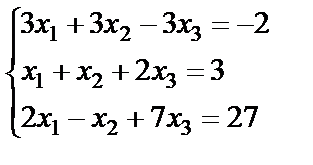 ; 20.
; 20. 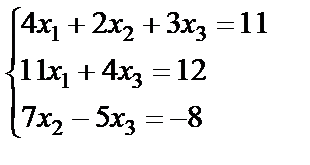
Задание 3. Решите систему линейных уравнений по формулам
Крамера.
1. 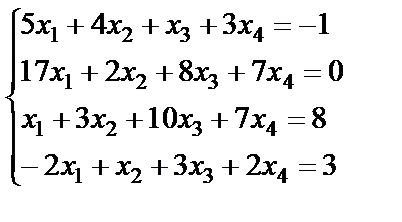 ; 2.
; 2. 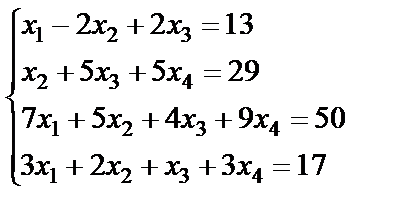 ;
;
3. 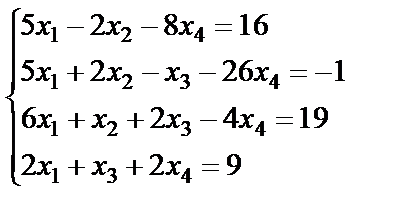 ; 4.
; 4. 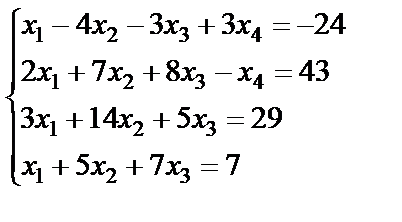 ;
;
5. 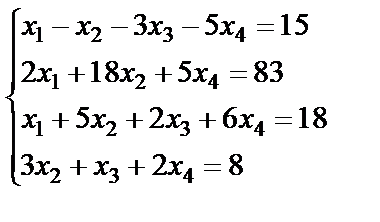 ; 6.
; 6. 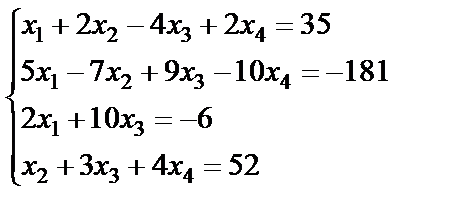 ;
;
7. 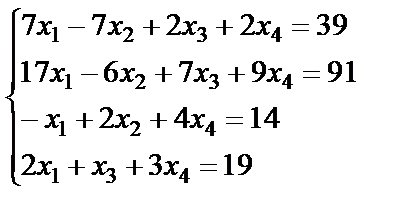 ; 8 .
; 8 . 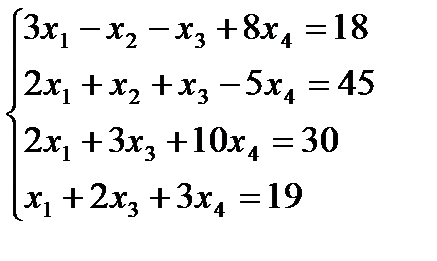 ;
;
9. 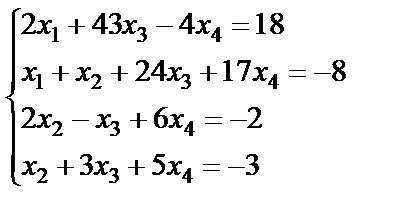 ; 10.
; 10. 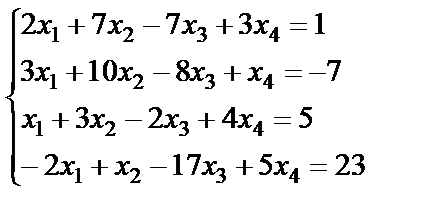 ;
;
11. 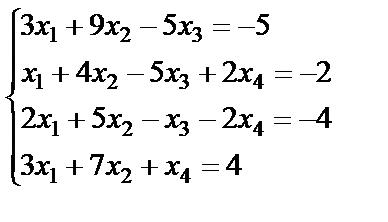 ; 12.
; 12. 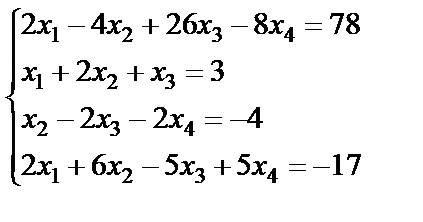 ;
;
13. 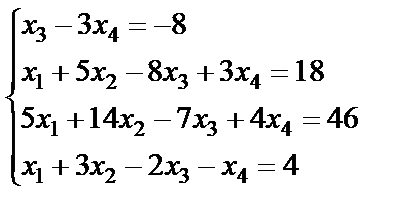 ; 14.
; 14. 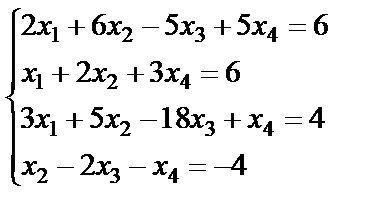 ;
;
15. 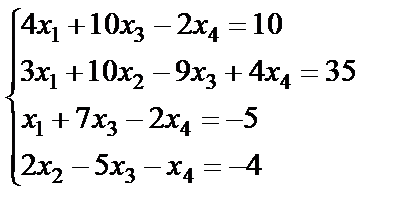 ; 16.
; 16. 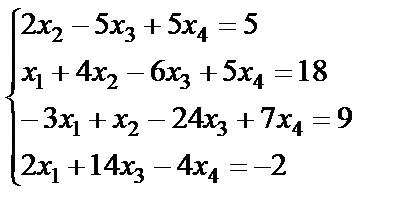 ;
;
17. 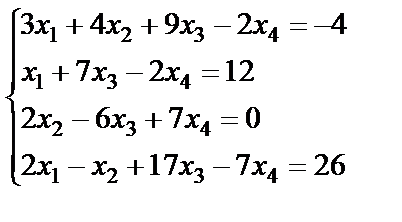 ; 18.
; 18. 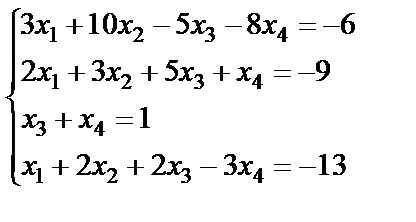 ;
;
19. 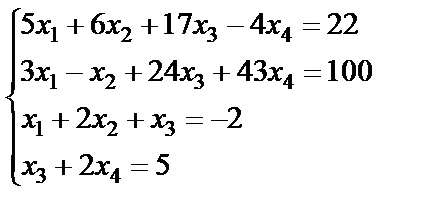 ; 20.
; 20. 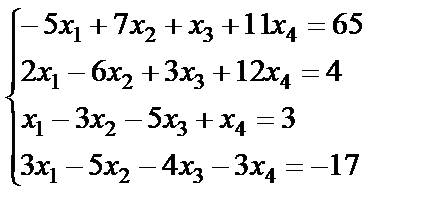
Задание 4. Найдите все решения однородной системы линейных уравнений методом Гаусса.
1.  ; 2.
; 2. 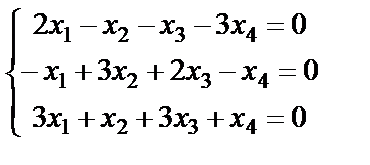 ;
;
3. 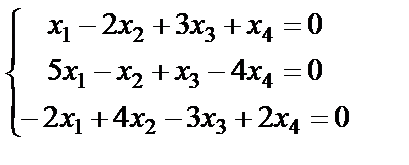 ; 4.
; 4. 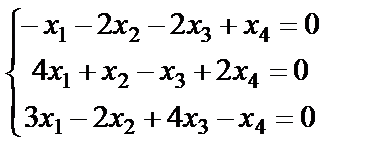 ;
;
5. 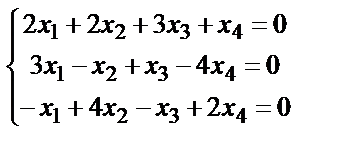 ; 6.
; 6. 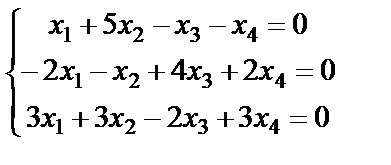 ;
;
7. 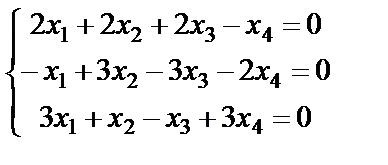 ; 8.
; 8. 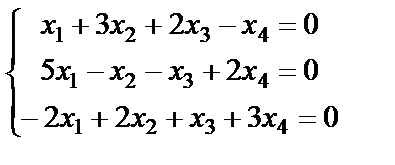 ;
;
9. 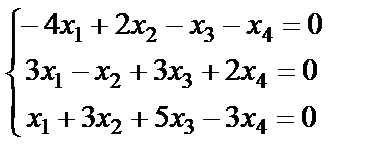 ; 10.
; 10. 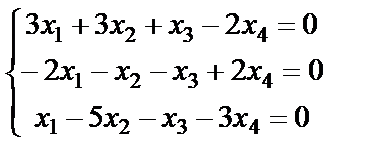 ;
;
11. 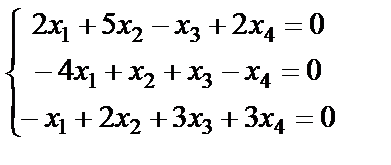 ; 12.
; 12. 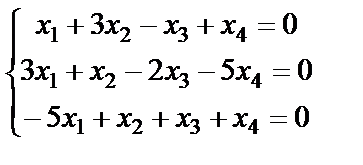 ;
;
13. 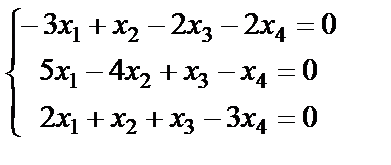 ; 14.
; 14. 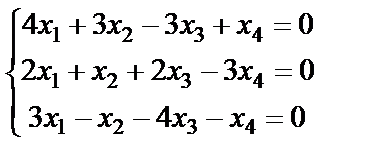 ;
;
15.  ; 16
; 16 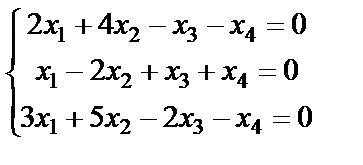 ;
;
17. 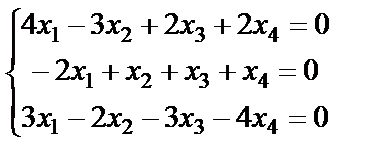 ; 18.
; 18. 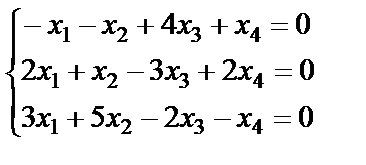 ;
;
19. 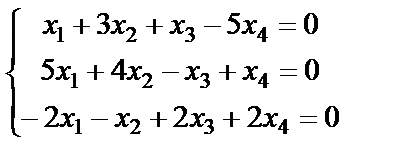 ; 20.
; 20. 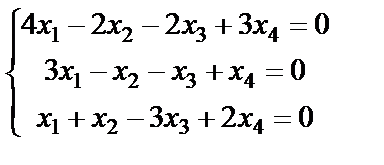
Задание 5
По координатам вершин пирамиды а1 а2 а3 а4 найти:
1) длины ребер а1 а2 и а1 а3;
2) угол между ребрами а1 а2 и а1 аз;
3) площадь грани а1 а2 а3;
4) объем пирамиды а1 а2 а3 а4;
5) уравнения прямых а1 а2 иа1 а3;
6) уравнения плоской а1 а2 а3 иа1 а2 а4 ;
7) угол между плоскостями а1 а2 а3 иа1 а2 а4;
8) угол между ребром а1 а3 и гранью а1 а2 а4 ;
9) уравнение высоты, опущенной из вершины а4 на грань а1 а2 а3 ;
10) уравнение плоскости, проходящей через высоту пирамиды, опущенную из вершины а4 на грань а1 а2 а3 , и вершину а1 пирамиды ;
11) расстояние от вершины.а3до плоскости а1 а2 а4.
| а1 | а2 | а3 | а4 | |
| (3;1;4) | (-1;6;1) | (-1;1;6) | (0;4;-1) | |
| (3;3;9) | (6;9;1) | (1;7;3) | (8;5;8) | |
| (3;5;4) | (5;8;3) | (1;9;9) | (6;4;8) | |
| (2;4;3) | (7;6;3) | (4;9;3) | (3;6;7) | |
| (9;5;5) | (-3;7;1) | (5;7;8) | (6;9;2) | |
| (0;7;1) | (4;1;5) | (4;6;3) | (3;9;8) | |
| (5;5;4) | (3;8;4) | (3;5;10) | (5;8;2) | |
| (6;1;1) | (4;6;6) | (4;2;0) | (1;2;6) | |
| (7;5;3) | (9;4;4) | (4;5;7) | (7;9;6) | |
| (6;6;2) | (5;4;7) | (2;4;7) | (7;3;0) | |
| (0;3;2) | (-1;3;6) | (-2;4;2) | (0;5;4) | |
| (-1;2;0) | (-2;2;4) | (-3;3;0) | (-1;4;2) | |
| (2;2;3) | (1;2;7) | (0;3;3) | (2;4;5) | |
| (0;-1;2) | (-1;-1;6) | (-2;0;2) | (0;1;4) | |
| (3;0;2) | (2;0;6) | (1;1;2) | (3;2;4) | |
| (0;2;-1) | (-1;2;3) | (-2;3;-1) | (0;4;1) | |
| (2;3;2) | (1;3;6) | (0;4;2) | (2;5;4) | |
| (-1;0;2) | (-2;0;6) | (-3;1;2) | (-1;2;4) | |
| (2;0;3) | (1;0;7) | (0;1;3) | (2;2;5) | |
| (2;-1;2) | (1;-1;6) | (0;0;2) | (2;1;4) |
Задание 6
Составить общее уравнение плоскости, проходящей через точку М перпендикулярно плоскостям a и b:
| M | a | b | |
| (2;1;-5) | 3X-2Y+Z+7=0 | 5X-4Y+3Z+1=0 | |
| (1;-1;1) | X-Y+Z-1=0 | 2X+Y+Z+1=0 | |
| (2;-1;1) | 3X+2Y-Z+4=0 | X+Y+Z-3=0 | |
| (1;8;2) | 5X+6Y+11Z-3=0 | 3X+Y+4Z-12=0 | |
| (-1;-2;0) | 4X+6Y-5Z-14=0 | X+3Y-2Z-1 =0 | |
| (5;1;2) | X-7Y-2Z-10=0 | 2X-2Y-Z-13=0 | |
| (2;4;1) | X-2Y+5Z-7=0 | 2X-3Y+7Z-5=0 | |
| (1;1;1) | X-2Y+2Z+8=0 | 3X+5Y+7Z-1=0 | |
| (1;4;5) | X+Y+5Z+3=0 | 3X+2Y+8Z-9=0 | |
| (3;0;7) | X+Y+4Z=0 | 3X+2Y+7Z-2=0 |
Составить уравнение плоскости, проходящей через точки М1, М2 перпендикулярно плоскости a :
| М1 | М2 | a | |
| (2;-1;4) | (3;2;1) | X+Y+Z-3=0 | |
| (1;1;1) | (2;2;2) | X-Y-Z=0 | |
| (0;-5;0) | (0;0;2) | X+5Y+2Z-10=0 | |
| (2;0;-1) | (1;-1;3) | 3X+2Y-Z+3=0 | |
| (-1;-2;0) | (1;1;2) | X+2Y+2Z-4=0 | |
| (1;-2;4) | (2;-3;5) | X+Y-3Z+8=0 | |
| (0;1;3) | (1;2;7) | X+2Y+5Z+6=0 | |
| (1;1;0) | (2;-1;-1) | 5X+2Y+3Z-7=0 | |
| (1;4;0) | (2;14;3) | X+6Y+Z-3=0 | |
| (9;1;1) | (19;2;2) | 17X+2Y+Z+11=0 | |
| (7;1;0) | (26;2;3) | 9X+Y+Z-17=0 | |
| (0;1;2) | (-1;2;3) | X+Y-Z+2=0 | |
| (3;4;6) | (5;1;5) | X+2Y+3Z-6=0 | |
| (4;1;0) | (2;-1;1) | X-Y+Z-3=0 | |
| (1;0;1) | (-1;1;0) | X+2Y-Z-1=0 |
Задание 7
Найти проекцию точки А на плоскости a:
| А | a | |
| (1;3;1) | x+2y+2z-30=0 | |
| (3;1;-1) | 3x+y+z-20=0 | |
| (5;2;-1) | 2x-y+3z+23=0 | |
| (4;-3;1) | x-2y-z-15=0 | |
| (1;-1;0) | 5x-6y+2z-76=0 |
Найти точку, симметричную точке А относительно плоскости а:
| А | а | |
| (0;0;0;) | х-2у+4z-21=0 | |
| (1;5;2) | 2х-у-z+11=0 | |
| (1;-3;-4) | Зх-у-2z=0 | |
| (5;2;-1) | 2х-у+3z+23=0 | |
| (3;-4;-6) | 9х-7у-31z-108=0 |
Найти точку, симметричную точке А относительно прямой ℓ:
| А | ℓ | |
| (2;1;0) | 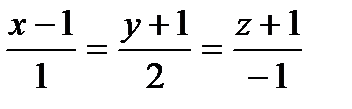
| |
| (4;3;10) | 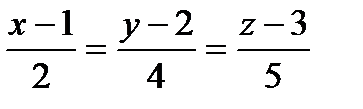
| |
| (1;-1;2) | 
| |
| (3;2;0) | 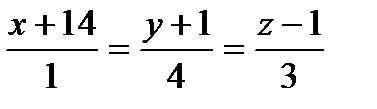
| |
| (2;-1;5) | 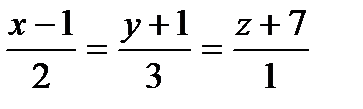
| |
| (0;0;0;) | 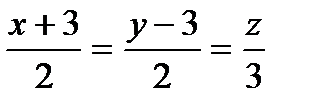
|
Составить уравнения прямой, проходящей через точки пересечения плоскостиа с прямыми ℓ1 и ℓ2:
| А | ℓ1 | ℓ2 | |
| 2x+y-3z=0 | 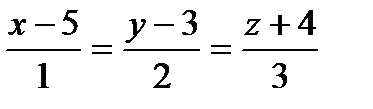
| 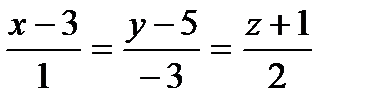
| |
| 3x-2y+z=0 | 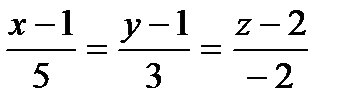
| 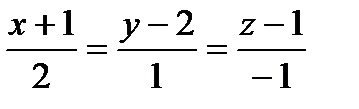
| |
| 6x+3y-41=0 | 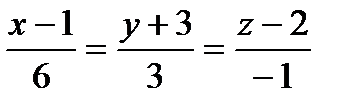
| 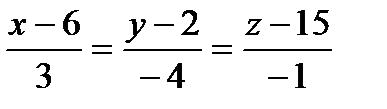
| |
| 3x-y-2z+5=0 | 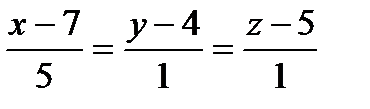
| 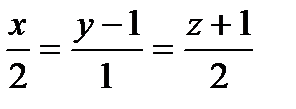
| |
| 2x+3y+z-1=0 | 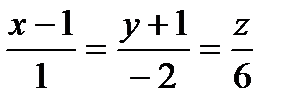
| 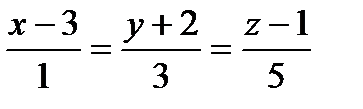
|
Составить уравнения прямой, лежащей в плоскости aи проходящей через точку пересечения плоскости a с прямой ℓ, перпендикулярно вектору `а:
| a | ℓ | _` а | |
| 6x+3y-z-41=0 | 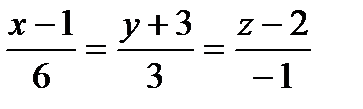
| {1;2;1} | |
| x+2y=0 | 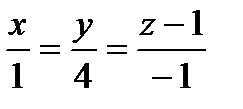
| {3;-1;2} | |
| x+2y=0 | 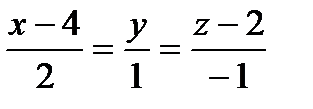
| {5;-1;2} | |
| 3x-y-2z+5=0 | 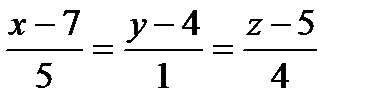
| {0;3;5} |
ЗАДАНИЕ 8
Вычислите пределы:
1 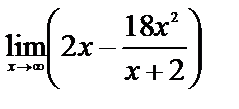
| 11 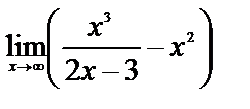
|
2 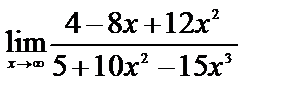
| 12 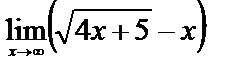
|
3 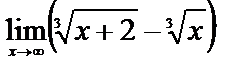
| 13 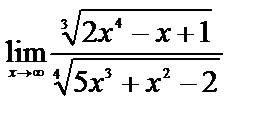
|
4 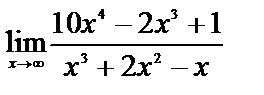
| 14 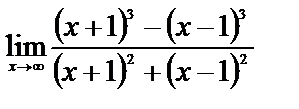
|
5 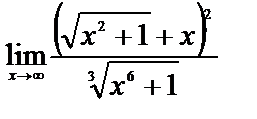
| |
6 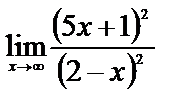
| |
7 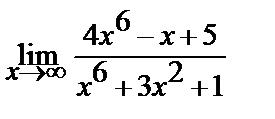
| |
8 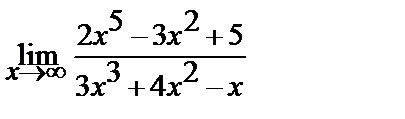
| |
9 
| |
10 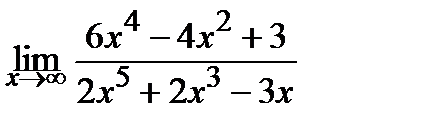
| |
15 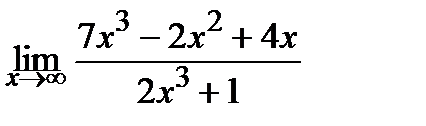
| |
16 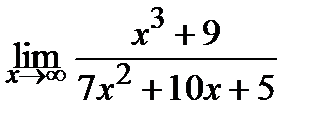
| |
17 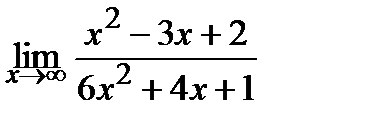 18
18 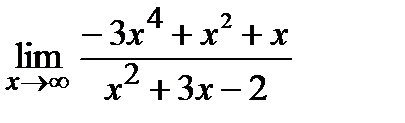
| |
19 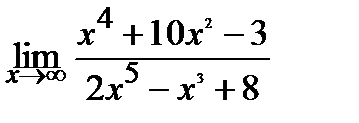
| |
| 20 | |
ЗАДАНИЕ 9
Вычислите пределы:
1 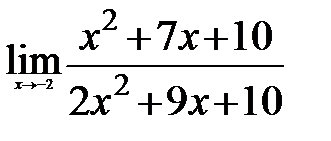
| 11 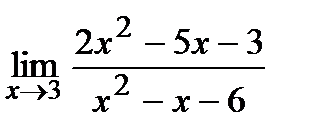
| |
2 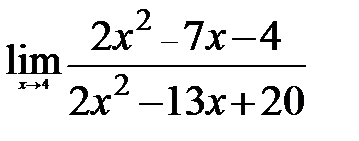
| 12 
| |
3 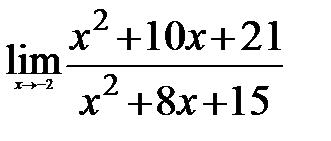
| 13 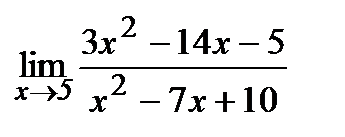
| |
4 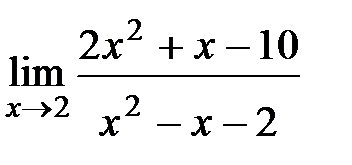
| 14 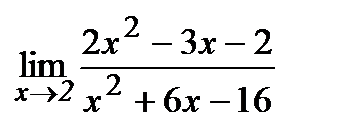
| |
5 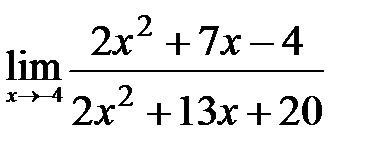
| 15 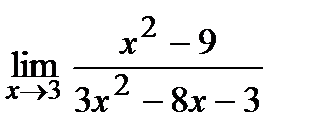
| |
6 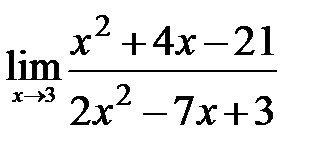
| 16 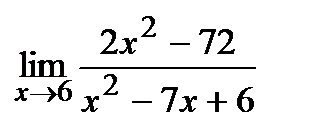
| |
7 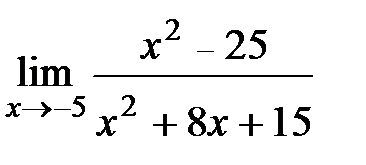
| 17 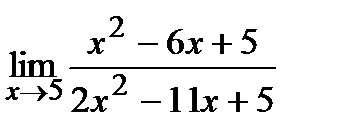
| |
8 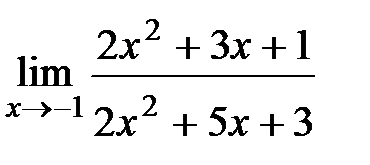
| 18 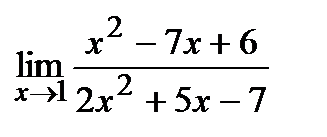
| |
9 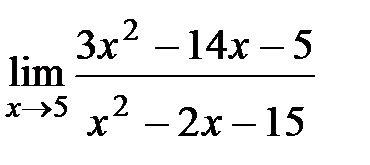
| 19 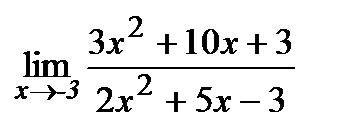
| |
10 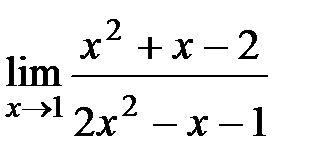
| 20 | |
ЗАДАНИЕ 10
Вычислите пределы:
а)
1 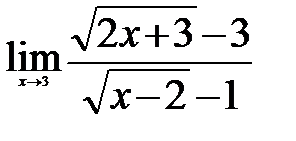
| 11 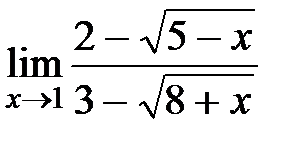
| |
2 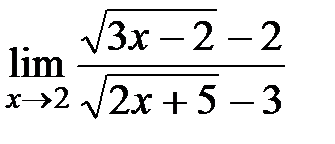
| 12 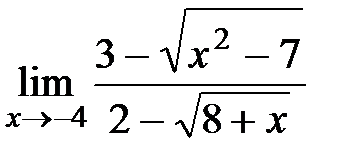
| |
3 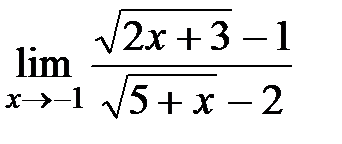
| 13 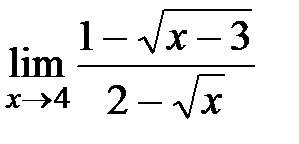
| |
4 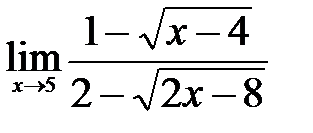
| 14 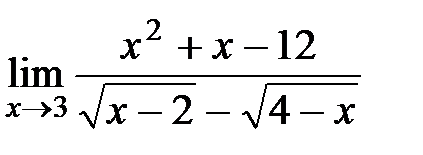
| |
5 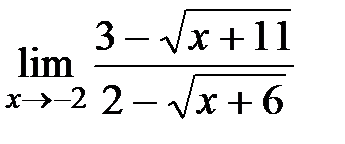
| 15 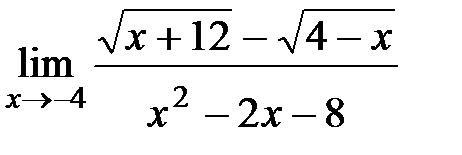
| |
6 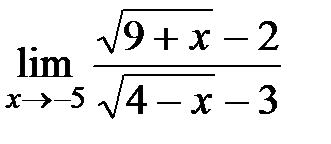
| 16 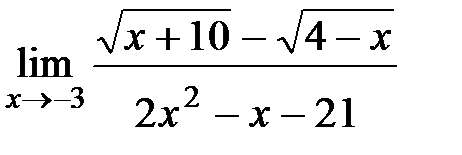
| |
7 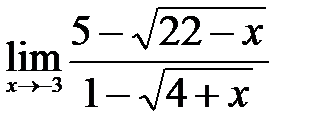
| 17 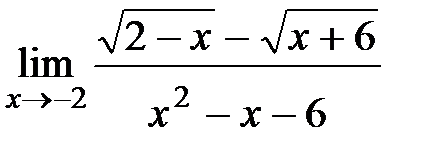
| |
8 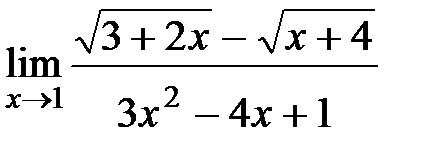
| 18 | |
9 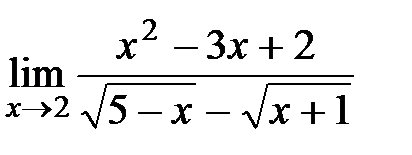
| 19 | |
10 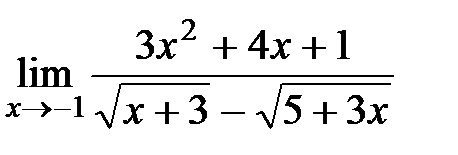
| 20 | |
б)
1 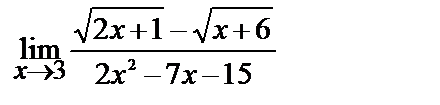
| 11 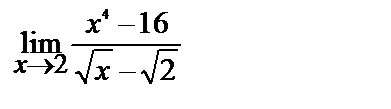
|
2 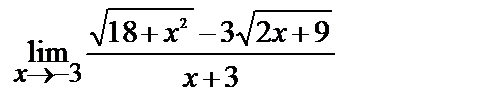
| 12 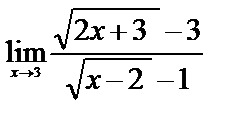
|
3 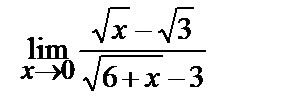
| 13 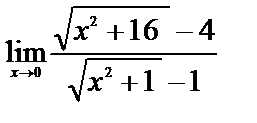
|
4 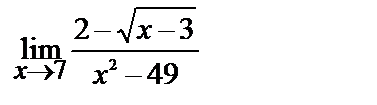
| 14 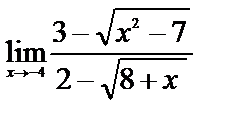
|
5 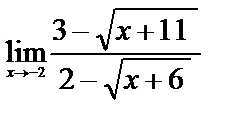
| 15 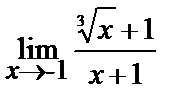
|
6 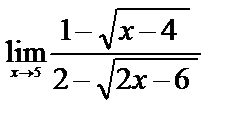
| 16 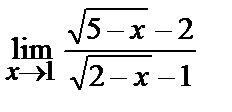
|
7 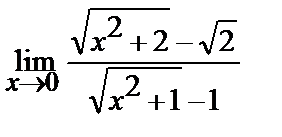
| 17 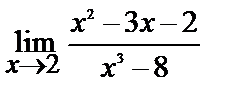
|
8 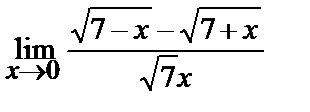
| 18 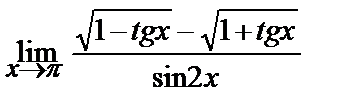
|
9 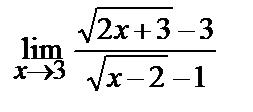
| 19 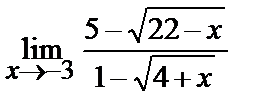
|
10 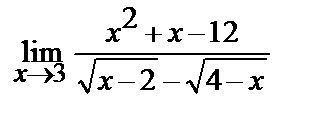
| 20 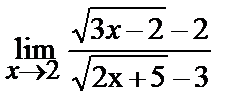
|
ЗАДАНИЕ 11
Вычислите пределы:
а)
1 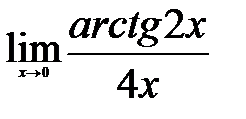
| 11 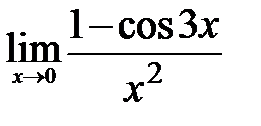
|
2 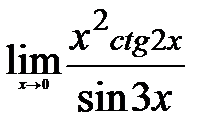
| 12 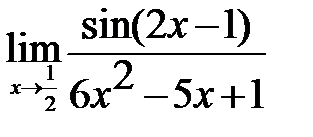
|
3 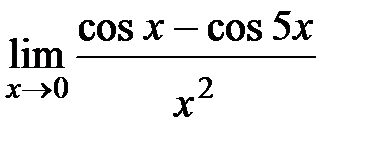
| 13 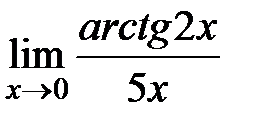
|
4 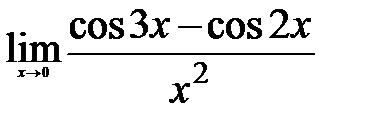
| 14 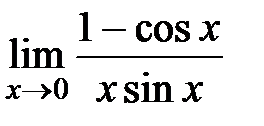
|
5 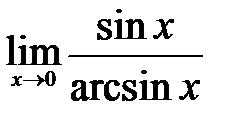
| 15 
|
6 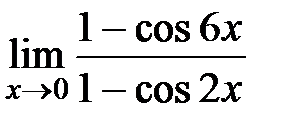
| 16 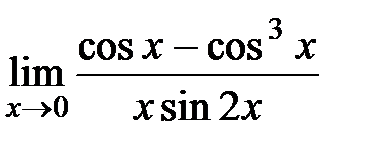
|
7 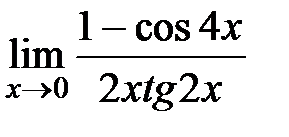
| 17 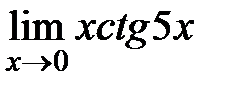
|
8 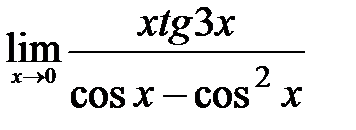
| 18 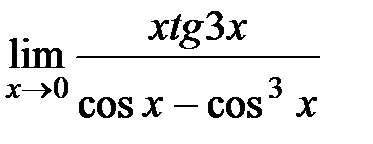
|
9 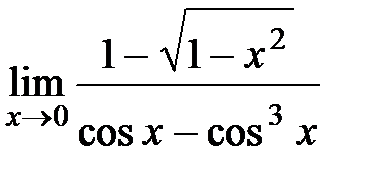
| 19 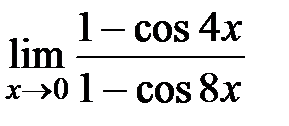
|
10 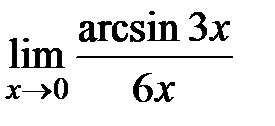
| 20 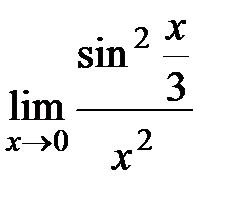
|
б)
1 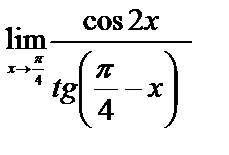
| 11 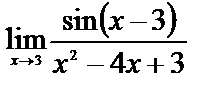
|
2 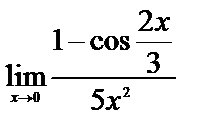
| 12 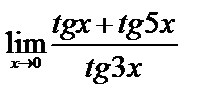
|
3 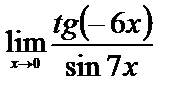
| 13 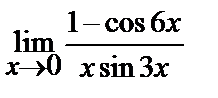
|
4 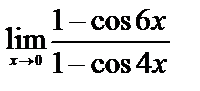
| 14 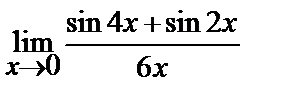
|
5 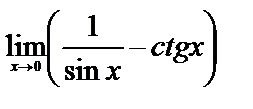
| 15 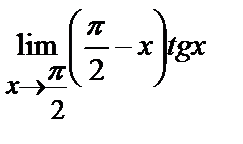
|
6 
| 16 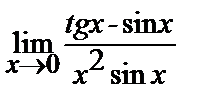
|
7 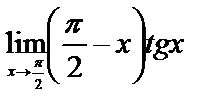
| 17 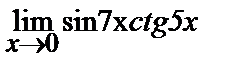
|
8 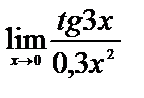
| 18 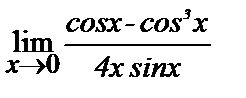
|
9 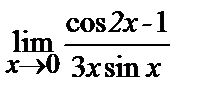
| 19 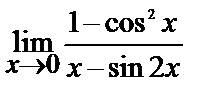
|
10 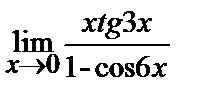
| 20 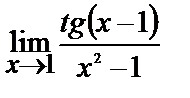
|
ЗАДАНИЕ 12
Вычислите пределы:
1 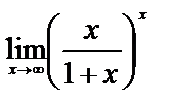
| 11 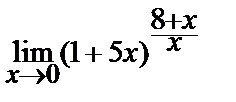
|
2 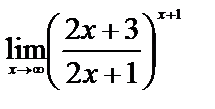
| 12. 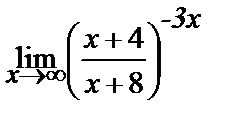
|
3 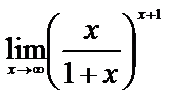
| 13 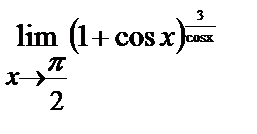
|
4 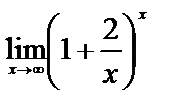
| 14 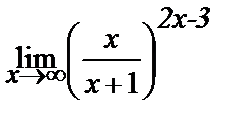
|
5 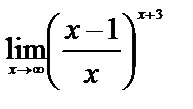
| 15 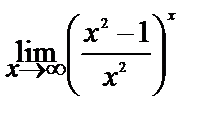
|
6 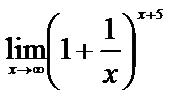
| 16 
|
7 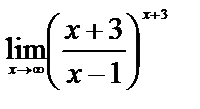
| 17 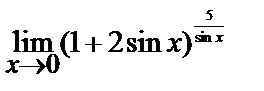
|
8 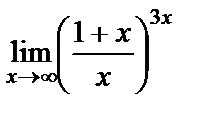
| 18 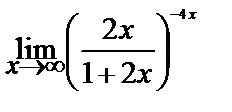
|
9 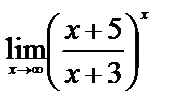
| 19 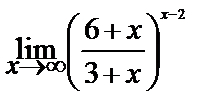
|
10 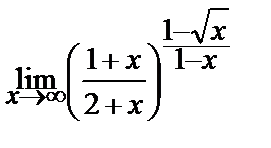
| 20 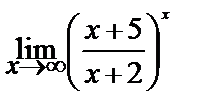
|
ЗАДАНИЕ 13
Исследуйте функции на непрерывность, найдите точки разрыва, если они существуют, установите их характер, постройте графики функций:
1 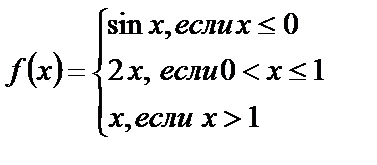
| 11 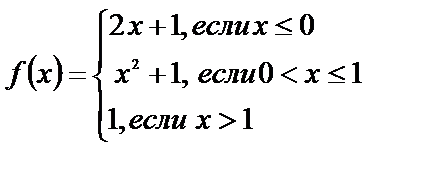
|
2 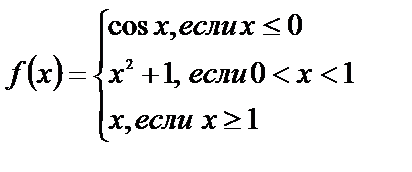
| 12 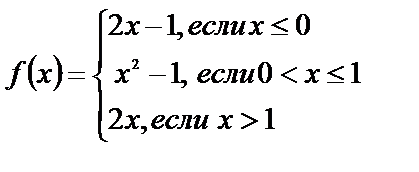
|
3 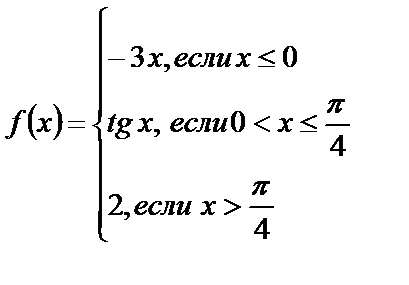
| 13 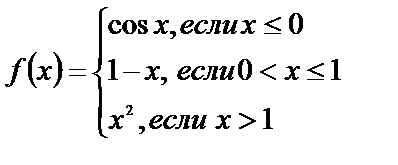
|
4 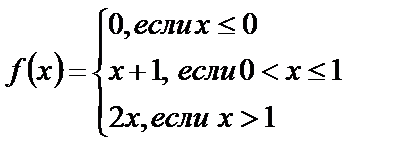
| 14 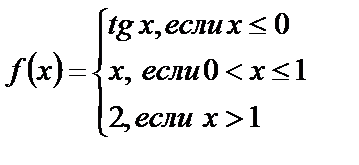
|
5 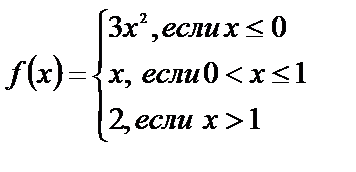
| 15 
|
6 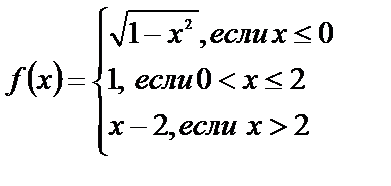
| 16 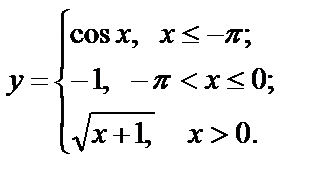
|
7 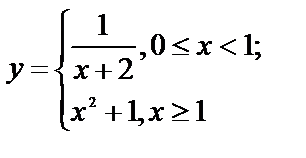
| 17 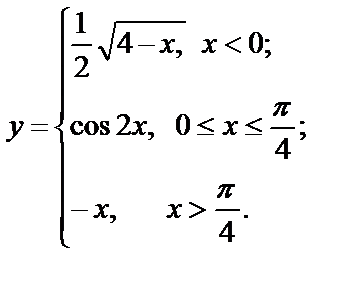
|
8 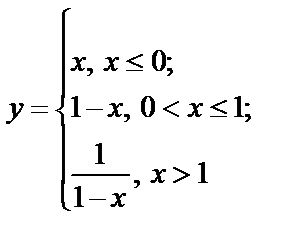
| 18 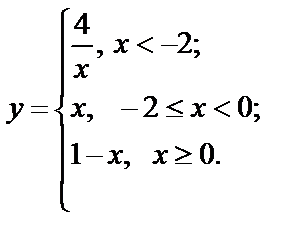
|
9 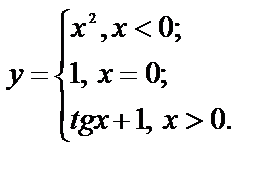
| 19 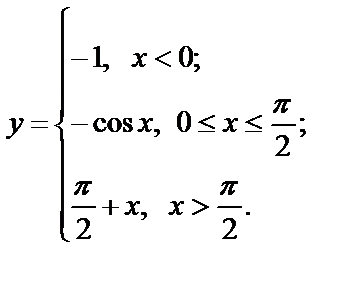
|
10 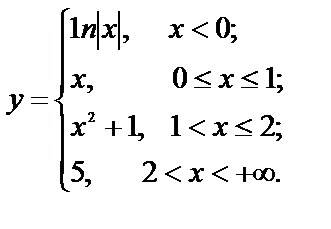
| 20 
|
ЗАДАНИЕ 14
Найти производную 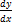 данной функции.
данной функции.
1. 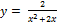 ;
;
2. 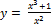 ;
;
3. 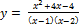 ;
;
4. 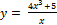 ;
;
5. 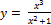 ;
;
6. 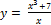 ;
;
7. 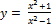 ;
;
8. 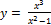 ;
;
9. 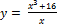 ;
;
10. 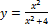 ;
;
11. 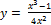 ;
;
12. 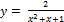 ;
;
13. 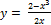 ;
;
14. 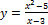 ;
;
15. 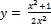 ;
;
16.  ;
;
17. 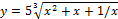 ;
;
18. 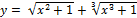 ;
;
19. 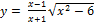 ;
;
20. 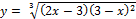 .
.
ЗАДАНИЕ 15
Найти производную 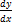 и
и 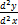 данной функции.
данной функции. 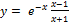 ;
;
2. 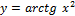 ;
;
3. 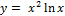 ;
;
4. 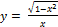 ;
;
5. 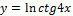 ;
;
6. 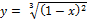 ;
;
7. 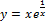 ;
;
8. 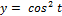 ;
;
9. 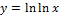 ;
;
10. 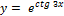 ;
;
11. 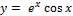 ;
;
12. 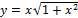 ;
;
13. 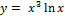 ;
;
14. 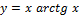 ;
;
15. 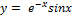 ;
;
16. 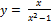 ;
;
17. 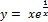 ;
;
18. 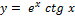 ;
;
19. 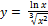 ;
;
20. 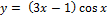 .
.
ЗАДАНИЕ 16
Найти наибольшее и наименьшее значение функции y = f (x) на отрезке [a, b].
1. 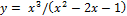 [4;6];
[4;6];
2. 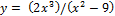 [4;6];
[4;6];
3. 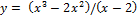 [-1;1];
[-1;1];
4. 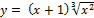 [-1;3];
[-1;3];
5. 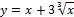 [-10;1];
[-10;1];
6. 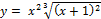 [-2;1];
[-2;1];
7. 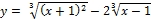 [-2;4];
[-2;4];
8. 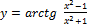 [-1;2];
[-1;2];
9. 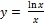 [1;4];
[1;4];
10. 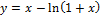 [-0.5;2];
[-0.5;2];
11. 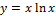 [
[ 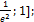
12. 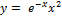 [-1;4];
[-1;4];
13. 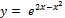 [-2;2];
[-2;2];
14. 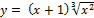 [-1;3];
[-1;3];
15. 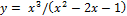 [4;6];
[4;6];
16. 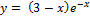 [0;5];
[0;5];
17. 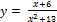 [-5;5];
[-5;5];
18. 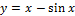 [-π;π];
[-π;π];
19. 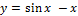 [
[ 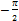 ;
;  ];
];
20. 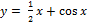 [0;
[0;  ].
].
ЗАДАНИЕ 17
Найти пределы, пользуясь правилом Лопиталя.
1. 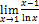 ;
;
2. 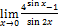 ;
;
3. 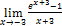 ;
;
4. 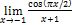 ;
;
5. 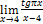 ;
;
6. 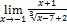 ;
;
7. 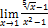 ;
;
8. 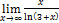 ;
;
9. 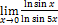 ;
;
10. 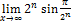 ;
;
11. 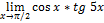
12. 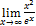 ;
;
13. 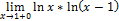 ;
;
14. 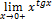 ;
;
15. 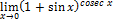 ;
;
16. 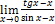 ;
;
17.  ;
;
18. 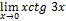 ;
;
19. 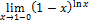 ;
;
20.  .
.
ЗАДАНИЕ 18
Найти частные производные 1 и 2 порядков от заданных функций.
1. 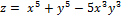 ;
;
2. 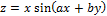 ;
;
3. 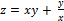 ;
;
4. 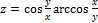 ;
;
5. 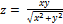 ;
;
6. 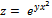 ;
;
7. 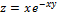 ;
;
8. 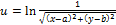 ;
;
9. 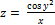 ;
;
10. 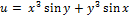 ;
;
11. 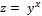 ;
;
12. 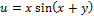 ;
;
13. 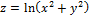 ;
;
14. 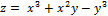 ;
;
15. 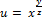 ;
;
16. 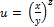 ;
;
17. 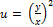 ;
;
18. 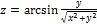 ;
;
19. 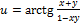 ;
;
20. 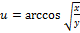 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|