
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПЛАН ЛЕКЦИИ. I. Теоремы сложения и умножения вероятностей. II. Формула полной вероятности. III. Формула Байеса
ПЛАН ЛЕКЦИИ
I. Теоремы сложения и умножения вероятностей
II. Формула полной вероятности
III. Формула Байеса
I. Теоремы сложения и умножения вероятностей. Суммой 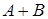 двух событий
двух событий 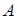 и
и 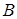 называется событие, состоящее в появлении события
называется событие, состоящее в появлении события 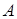 , или события
, или события 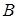 , или обоих этих событий.
, или обоих этих событий.
Пример 1. Производится бросок игрального кубика. Событие 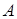 – выпадение четного числа очков (2, 4 или 6). Событие
– выпадение четного числа очков (2, 4 или 6). Событие 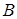 – выпадение числа очков, кратного трем (3 или 6). Суммой
– выпадение числа очков, кратного трем (3 или 6). Суммой 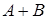 этих событий будет выпадение числа очков, кратного двум ИЛИ трем (2, 3, 4 или 6).
этих событий будет выпадение числа очков, кратного двум ИЛИ трем (2, 3, 4 или 6).
Если события 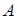 и
и 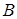 несовместные, то
несовместные, то 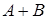 – событие, состоящее в появлении одного из этих событий, безразлично какого.
– событие, состоящее в появлении одного из этих событий, безразлично какого.
Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие 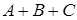 состоит в появлении одного из следующих событий:
состоит в появлении одного из следующих событий: 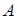 ,
, 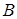 ,
, 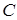 ,
, 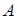 и
и 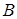 ,
, 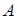 и
и 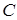 ,
, 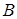 и
и 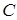 ,
, 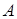 и
и 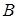 и
и 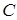 .
.
Теорема 1 (теорема сложения вероятностей несовместных событий): вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
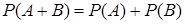 .
.
Доказательство.
По классическому определению вероятности, 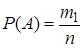 – вероятность события
– вероятность события 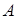 ,
, 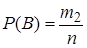 , вероятность события
, вероятность события 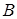 . Число элементарных исходов, благоприятствующих наступлению или события
. Число элементарных исходов, благоприятствующих наступлению или события 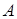 , или события
, или события 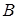 , равно
, равно 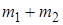 . Тогда вероятность события
. Тогда вероятность события 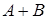
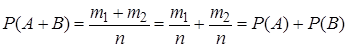 .
.
Теорема доказана.
Следствие: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
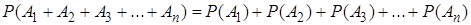 .
.
Доказательство.
Проведем доказательство для трех попарно несовместных событий 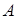 ,
, 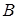 ,
, 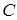 . События
. События 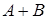 и
и 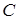 несовместны, поэтому к ним можно применить теорему 1:
несовместны, поэтому к ним можно применить теорему 1: 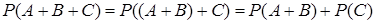 . События
. События 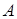 и
и 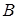 также несовместны, тогда по теореме 1
также несовместны, тогда по теореме 1
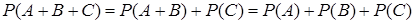 .
.
Доказательство для большего числа попарно несовместных событий аналогично.
Пример 2. В урне 30 шаров: 10 красных, 5 синих, 15 белых. Наудачу извлекают один шар. Найти вероятность появления цветного шара. (Здесь и далее будем называть цветным шар любого цвета кроме белого.)
Решение. Цветной шар – красный ИЛИ синий. Событие 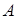 – из урны извлечен красный шар,
– из урны извлечен красный шар, 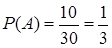 . Событие
. Событие 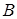 – из урны извлечен синий шар,
– из урны извлечен синий шар, 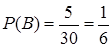 . Событие
. Событие 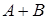 – из урны извлечен цветной шар. События
– из урны извлечен цветной шар. События 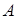 и
и 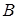 несовместны, тогда по теореме сложения несовместных событий:
несовместны, тогда по теореме сложения несовместных событий:
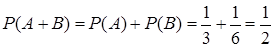 .
.
С другой стороны, число элементарных исходов, благоприятных для появления цветного шара, 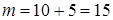 . Тогда, по определению вероятности,
. Тогда, по определению вероятности,
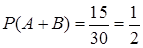 .
.
Ответ: 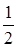 .
.
Теорема 2: сумма вероятностей событий 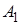 ,
, 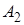 , …,
, …, 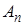 , образующих полную группу, равна единице,
, образующих полную группу, равна единице,
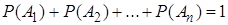 .
.
Доказательство.
Появление одного из событий полной группы достоверно, так как в одном испытании обязательно должно наступить одно из событий 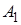 ,
, 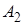 , …,
, …, 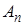 , образующих полную группу. Вероятность достоверного события равна единице:
, образующих полную группу. Вероятность достоверного события равна единице:
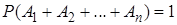 . (1)
. (1)
События полной группы попарно несовместны, и по теореме сложения вероятностей несовместных событий
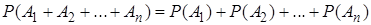 . (2)
. (2)
Сравнивая выражения (1) и (2), получим
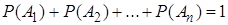 .
.
Теорема доказана.
Противоположными называются два единственно возможных события, образующих полную группу.
Примеры противоположных событий: 1) выпадение герба и выпадение цифры при одном броске монеты; 2) попадание и промах при одном выстреле по мишени.
Событие, противоположное событию 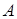 , обозначается
, обозначается 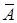 .
.
Теорема 3: сумма вероятностей противоположных событий равна единице:
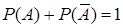 .
.
Доказательство.
Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице. Теорема доказана.
Часто вероятность одного из двух противоположных событий обозначают 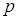 , а другого –
, а другого – 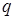 . Тогда в силу предыдущей теоремы
. Тогда в силу предыдущей теоремы 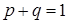 .
.
При решении задач на отыскание вероятности события 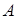 бывает удобно сначала вычислить вероятность противоположного события
бывает удобно сначала вычислить вероятность противоположного события 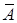 , а потом найти вероятность события
, а потом найти вероятность события 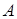 по формуле, следующей из теоремы 3:
по формуле, следующей из теоремы 3:
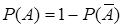 . (3)
. (3)
Пример 3. В урне 50 шаров: 10 красных, 5 синих, 15 желтых, 20 белых. Наудачу извлекают один шар. Найти вероятность появления цветного шара.
Решение. Событие 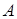 – из урны извлечен цветной шар (безразлично, красный, синий или желтый), тогда противоположное событие
– из урны извлечен цветной шар (безразлично, красный, синий или желтый), тогда противоположное событие 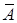 – из урны извлечен белый шар,
– из урны извлечен белый шар, 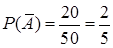 . По формуле (3)
. По формуле (3) 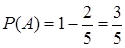 .
.
Ответ: 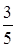 .
.
Произведением двух событий 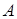 и
и 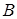 называется событие
называется событие 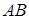 , состоящее в совместном появлении этих событий. Например, если событие
, состоящее в совместном появлении этих событий. Например, если событие 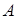 – деталь стандартная, событие
– деталь стандартная, событие 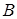 – деталь окрашенная, то событие
– деталь окрашенная, то событие 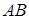 – деталь годная и окрашенная.
– деталь годная и окрашенная.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Условной вероятностью 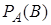 называется вероятность события
называется вероятность события 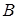 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 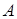 уже наступило.
уже наступило.
Условная вероятность события 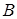 при условии, что событие
при условии, что событие 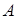 уже наступило, определяется по формуле
уже наступило, определяется по формуле
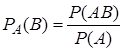 . (4)
. (4)
В выражении (4) 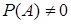 , так как событие
, так как событие 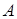 уже наступило.
уже наступило.
Теорема 4 (теорема умножения вероятностей): вероятность появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило,
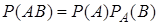 . (5)
. (5)
Доказательство.
По определению условной вероятности, 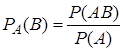 . Из этой формулы выражается вероятность события
. Из этой формулы выражается вероятность события 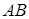 :
: 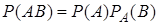 . Теорема доказана.
. Теорема доказана.
Вероятность события 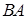
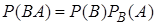 . Событие
. Событие 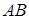 не отличается от события
не отличается от события 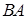 , поэтому
, поэтому 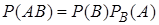 , тогда
, тогда
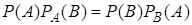 . (6)
. (6)
Следствие теоремы умножения вероятностей: вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
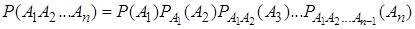 . (7)
. (7)
Порядок, в котором расположены события, может быть выбран любым, то есть безразлично, какое событие считать первым, какое вторым и т.д.
Пример 4. В ящике лежат 4 тетради в клетку и 6 в линейку. Школьник наугад взял одну тетрадь, а затем вторую. Найти вероятность того, что первой взята тетрадь в клетку, а второй – в линейку.
Решение. Событие 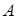 – первой взята тетрадь в клетку,
– первой взята тетрадь в клетку, 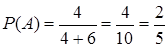 . Событие
. Событие 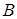 – второй взята тетрадь в линейку. Вычислим вероятность этого события в предположении, что событие
– второй взята тетрадь в линейку. Вычислим вероятность этого события в предположении, что событие 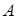 наступило, то есть его условную вероятность
наступило, то есть его условную вероятность 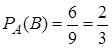 . Вероятность события
. Вероятность события 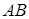 (первой взята тетрадь в клетку, а второй – в линейку) по теореме умножения вероятностей
(первой взята тетрадь в клетку, а второй – в линейку) по теореме умножения вероятностей 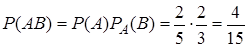 .
.
Ответ: 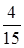 .
.
Событие 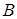 называется независимым от события
называется независимым от события 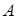 , если появление события
, если появление события 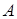 не изменяет вероятности события
не изменяет вероятности события 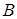 , то есть если условная вероятность события
, то есть если условная вероятность события 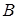 равна его безусловной вероятности:
равна его безусловной вероятности:
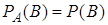 . (8)
. (8)
Подставим выражение (8) в соотношение (6):
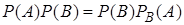 .
.
Тогда
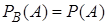 , (9)
, (9)
то есть для независимых событий условная вероятность события 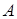 в предположении, что наступило событие
в предположении, что наступило событие 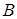 , равно его безусловной вероятности.
, равно его безусловной вероятности.
Теорема 5 (теорема умножения вероятностей независимых событий): вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий
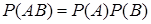 . (10)
. (10)
Два события называются независимыми, если вероятность их совместного появления равна произведению вероятностей этих событий. В противном случае события называются зависимыми.
Пример 5. В первом ящике 300 болтов, из которых 75 с резьбой М12, а остальные с резьбой М10. Во втором ящике 200 гаек, из которых 80 с резьбой М12, а остальные с резьбой М14. Рабочий берет наудачу один болт и одну гайку. Найти вероятность того, что они подойдут друг другу.
Решение. Событие 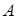 – резьба взятого болта М12,
– резьба взятого болта М12, 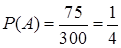 . Событие
. Событие 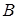 – резьба взятой гайки М12,
– резьба взятой гайки М12, 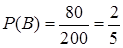 . Болт и гайка подойдут друг другу, если будут иметь резьбу М12, то есть если наступит событие
. Болт и гайка подойдут друг другу, если будут иметь резьбу М12, то есть если наступит событие 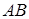 . События
. События 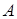 и
и 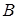 независимые, тогда по теореме 5
независимые, тогда по теореме 5 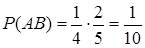 .
.
Ответ: 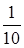 .
.
Если события 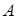 и
и 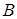 независимы, то независимы также события
независимы, то независимы также события 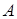 и
и 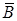 ,
, 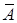 и
и 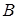 ,
, 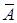 и
и 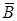 .
.
Несколько событий называются попарно независимыми, если каждые два из них независимы.
Несколько событий называются независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных событий. Например, если события  ,
, 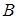 и
и 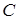 независимы в совокупности, то независимы события
независимы в совокупности, то независимы события  и
и 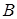 ,
,  и
и 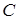 ,
, 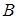 и
и 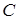 ,
,  и
и 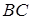 ,
, 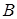 и
и 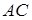 ,
, 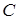 и
и 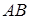 .
.
Следствие теоремы умножения независимых событий: вероятность появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
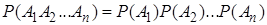 . (11)
. (11)
Если события 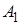 ,
, 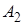 , …,
, …, 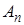 независимы в совокупности, то противоположные им события
независимы в совокупности, то противоположные им события 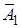 ,
, 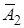 , …,
, …, 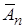 тоже независимы в совокупности.
тоже независимы в совокупности.
Пусть в результате испытания могут появиться 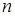 событий, независимых в совокупности, или некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Требуется определить вероятность наступления хотя бы одного из этих событий. Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий.
событий, независимых в совокупности, или некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Требуется определить вероятность наступления хотя бы одного из этих событий. Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий.
Теорема 6: вероятность появления хотя бы одного из событий 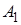 ,
, 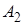 , …,
, …, 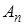 , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 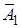 ,
, 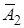 , …,
, …, 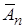 :
:
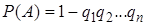 . (12)
. (12)
Доказательство.
Пусть событие  состоит в появлении хотя бы одного из событий
состоит в появлении хотя бы одного из событий 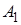 ,
, 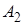 , …,
, …, 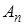 . Событие
. Событие 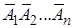 – ни одно из событий
– ни одно из событий 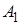 ,
, 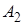 , …,
, …, 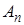 не наступило. События
не наступило. События  и
и 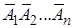 являются противоположными, следовательно, по теореме 3, сумма их вероятностей равна единице:
являются противоположными, следовательно, по теореме 3, сумма их вероятностей равна единице: 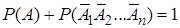 . Из этого равенства, используя теорему 5 умножения вероятностей для независимых событий, получим
. Из этого равенства, используя теорему 5 умножения вероятностей для независимых событий, получим
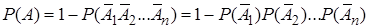
или
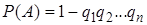 .
.
Теорема доказана.
Если события 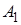 ,
, 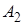 , …,
, …, 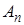 имеют одинаковые вероятности, равные
имеют одинаковые вероятности, равные 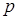 , то вероятность появления хотя бы одного из этих событий
, то вероятность появления хотя бы одного из этих событий
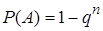 . (13)
. (13)
Пример 6. Четыре стрелка делают по одному выстрелу по мишени. Вероятности попадания в мишень для каждого из них равны 0,9, 0,8, 0,7 и 0,6. Найти вероятность того, что мишень поражена.
Решение.
Событие  – мишень поражена. Событие
– мишень поражена. Событие 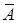 – мишень не поражена. Вероятности поражения мишени каждым стрелком соответственно равны
– мишень не поражена. Вероятности поражения мишени каждым стрелком соответственно равны 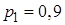 ,
, 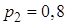 ,
, 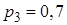 ,
, 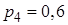 , а вероятности промаха
, а вероятности промаха 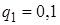 ,
, 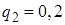 ,
, 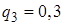 ,
, 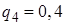 . Событие
. Событие 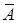 наступит, если все четыре стрелка промахнутся, то есть
наступит, если все четыре стрелка промахнутся, то есть 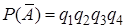 , тогда
, тогда
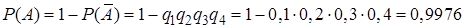 .
.
Ответ: 0,9976.
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример 7. Событие  – появление двух очков при одном броске игрального кубика. Событие
– появление двух очков при одном броске игрального кубика. Событие 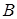 – появление четного числа очков. События
– появление четного числа очков. События  и
и 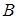 совместные.
совместные.
Теорема 7 (теорема сложения вероятностей совместных событий): вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
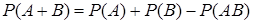 . (14)
. (14)
Доказательство.
По условию теоремы, события  и
и 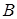 совместны. Поэтому событие
совместны. Поэтому событие 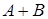 произойдет, если наступит одно из трех несовместных событий
произойдет, если наступит одно из трех несовместных событий 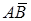 ,
, 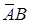 или
или 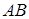 . По теореме 1 сложения вероятностей несовместных событий,
. По теореме 1 сложения вероятностей несовместных событий,
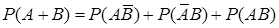 . (15)
. (15)
Событие  произойдет, если наступит одно из двух несовместных событий
произойдет, если наступит одно из двух несовместных событий 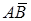 или
или 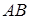 . По теореме 1 сложения вероятностей несовместных событий,
. По теореме 1 сложения вероятностей несовместных событий,
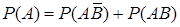 ,
,
откуда следует, что
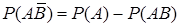 . (16)
. (16)
На основании этой же теоремы
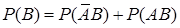 ,
,
откуда следует, что
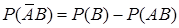 . (17)
. (17)
Подставляя выражения (16) и (17) в формулу (15), получим
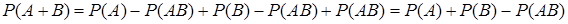 .
.
Теорема доказана.
Пример 8. Два орудия стреляют по цели, делая по одному выстрелу. Вероятность попадания для первого орудия равна 0,7, для второго – 0,6. Найти вероятность того, что цель поражена.
Решение.
Событие  – попадание в цель первого орудия,
– попадание в цель первого орудия, 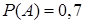 , событие
, событие 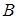 – попадание в цель второго орудия,
– попадание в цель второго орудия, 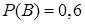 . События
. События  и
и 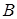 совместные, тогда по теореме 7
совместные, тогда по теореме 7 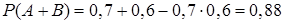 .
.
Ответ: 0,88.
II. Формула полной вероятности. Следствием теоремы сложения вероятностей и теоремы умножения вероятностей является формула полной вероятности.
Пусть событие  может наступить при условии наступления одного из несовместных событий
может наступить при условии наступления одного из несовместных событий 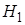 ,
, 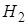 , …
, … 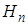 , которые образуют полную группу. Эти события называются гипотезами.
, которые образуют полную группу. Эти события называются гипотезами.
Теорема 8: вероятность события  , которое может наступить только при условии появления одного из несовместных событий
, которое может наступить только при условии появления одного из несовместных событий 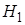 ,
, 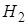 , …
, … 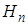 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события  :
:
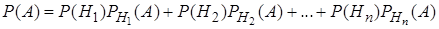 . (18)
. (18)
Доказательство.
Событие  может наступить, если наступит одно из несовместных событий
может наступить, если наступит одно из несовместных событий 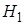 ,
, 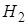 , …
, … 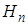 , то есть наступление события
, то есть наступление события  означает появление одного из несовместных событий
означает появление одного из несовместных событий 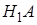 ,
, 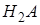 , …,
, …, 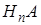 . По теореме 1 сложения вероятностей несовместных событий, вероятность события
. По теореме 1 сложения вероятностей несовместных событий, вероятность события 
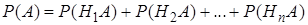 . (19)
. (19)
Преобразуем каждое слагаемое в правой части выражения (19), используя теорему 4 умножения вероятностей:
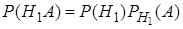 ,
, 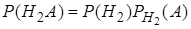 , …,
, …, 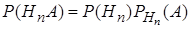 .
.
Подставим правые части этих равенств в формулу (19):
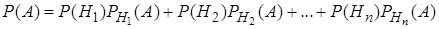 .
.
Теорема доказана.
Формула (18) называется формулой полной вероятности.
Пример 9. Имеется две урны с черными и белыми шарами. В первой урне 10 черных и 20 белых шаров, во второй – 20 черных и 10 белых. Найти вероятность того, что шар, наудачу извлеченный из наудачу взятой урны, будет белым.
Решение.
Событие  – наудачу извлеченный шар белый. Гипотеза
– наудачу извлеченный шар белый. Гипотеза 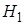 – шар взят из первой урны, гипотеза
– шар взят из первой урны, гипотеза 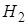 – шар взят из второй урны. Урна выбирается наудачу, поэтому вероятности гипотез одинаковы:
– шар взят из второй урны. Урна выбирается наудачу, поэтому вероятности гипотез одинаковы: 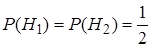 . Условные вероятности события
. Условные вероятности события  при каждой из введенных гипотез
при каждой из введенных гипотез 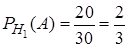 ,
, 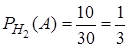 . Вероятность события
. Вероятность события  найдем по формуле полной вероятности:
найдем по формуле полной вероятности:
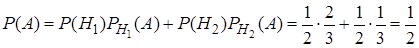 .
.
Ответ: 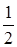 .
.
III. Формула Байеса. Пусть произведено испытание, в результате которого наступило событие  . Определим, как изменились вероятности гипотез в связи с тем, что событие
. Определим, как изменились вероятности гипотез в связи с тем, что событие  наступило, то есть будем искать условные вероятности
наступило, то есть будем искать условные вероятности 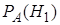 ,
, 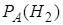 , …,
, …, 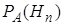 .
.
Найдем условную вероятность 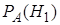 . По теореме умножения вероятностей 4 (формула (5)),
. По теореме умножения вероятностей 4 (формула (5)), 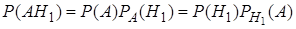 , откуда
, откуда
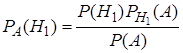 .
.
Заменяя 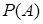 по формуле полной вероятности, получим
по формуле полной вероятности, получим
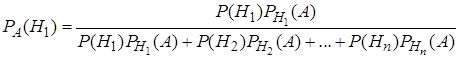 . (20)
. (20)
Аналогично может быть вычислена условная вероятность любой гипотезы 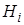 (
( 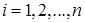 ):
):
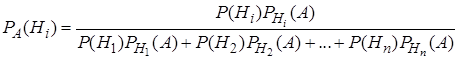 . (21)
. (21)
Полученные формулы (20), (21) называются формулами Байеса. Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие  .
.
Пример 10. Имеется две урны с черными и белыми шарами. В первой урне 10 черных и 20 белых шаров, во второй – 20 черных и 10 белых. Шар, наудачу извлеченный из наудачу взятой урны, оказался белым. Найти вероятность того, что он извлечен из первой урны.
Решение.
Событие  – наудачу извлеченный шар белый. Гипотеза
– наудачу извлеченный шар белый. Гипотеза 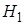 – шар взят из первой урны, гипотеза
– шар взят из первой урны, гипотеза 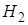 – шар взят из второй урны. Урна выбирается наудачу, поэтому вероятности гипотез одинаковы:
– шар взят из второй урны. Урна выбирается наудачу, поэтому вероятности гипотез одинаковы: 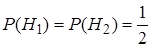 . Условные вероятности события
. Условные вероятности события  при каждой из введенных гипотез
при каждой из введенных гипотез 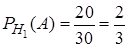 ,
, 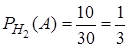 . Вероятность события
. Вероятность события 
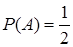 . Условную вероятность гипотезы
. Условную вероятность гипотезы 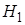
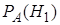 найдем по формуле Байеса (20):
найдем по формуле Байеса (20):
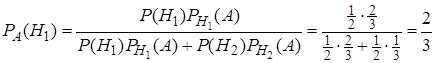 .
.
Ответ: 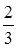 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|