Теорема.. Следствие 1.. Следствие 2.

Теорема.

Вероятность того, что отклонение выборочной средней (доли) от генеральной средней (доли) не превзойдет число D>0 (по модулю), равна

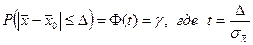
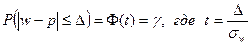, Ф(t) – функция Лапласа.

Следствие 1.

При заданной доверительной вероятности g предельная ошибка выборки равна t-кратной величине средней квадратической ошибки, где Ф(t)= g: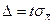

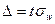
Следствие 2.

Доверительные интервалы для генеральной средней и генеральной доли находятся по формулам:

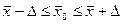
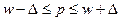
Если генеральная совокупность бесконечна или объем бесповторной выборки значительно меньше объема генеральной совокупности, расчеты средних квадратических ошибок для средней и доли и необходимого объема бесповторной выборки следует проводить по соответствующим формулам для повторной выборки.

⇐ Предыдущая 12