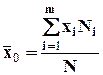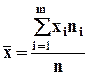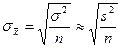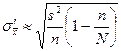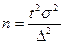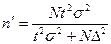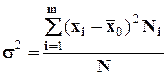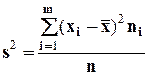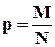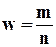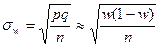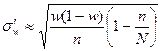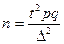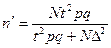Задание 1. Генеральная совокупность. Выборка. Средняя квадратическая ошибка выборки. Объем выборки

Население города составляет 20 000 человек. Выборка собственно-случайная бесповторная.

Распределение опрошенных по месячному доходу:

xi

менее 500

500-1000

1000-1500

1500-2000

2000-2500

свыше 2500

ni

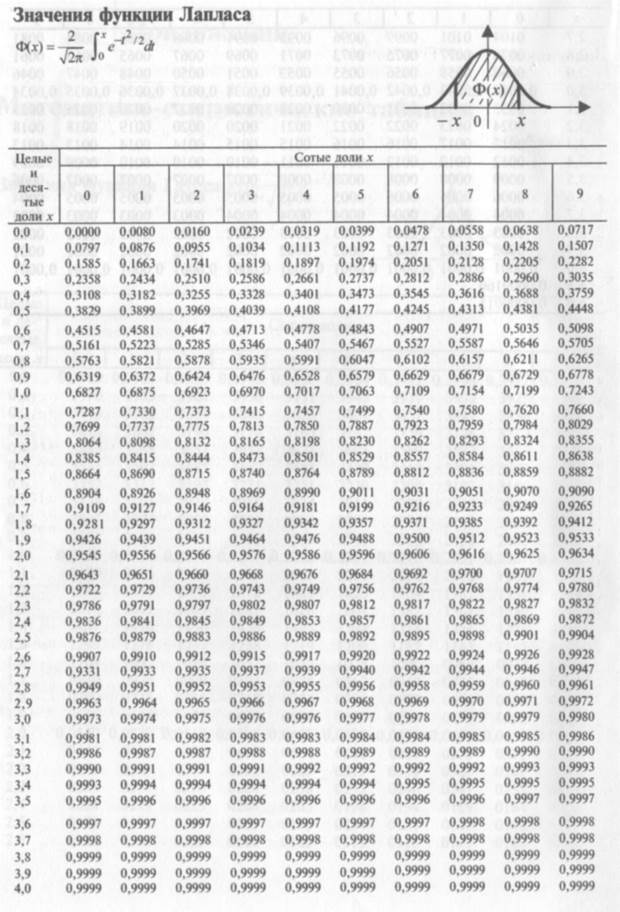
1. Найти вероятность того, что средний месячный доход жителя города отличается от среднего дохода в выборке не более, чем на 45 (по абсолютной величине)

2. Определить границы, в которых с надежностью 0,99 заключен средний месячный доход жителя города

3. Каким должен быть объем выборки, чтобы те же границы гарантировать с надежностью 0,9973?

4. Решить задачи 1 - 3, если население города неизвестно, но очень велико по сравнению с объемом выборки.

5. Найти вероятность того, что доля малообеспеченных жителей города (доход менее 500) отличается от доли таких же жителей в выборке не более, чем на 0,01 (по абсолютной величине)

6. Определить границы, в которых с надежностью 0,98 заключена доля малообеспеченных жителей города

7. Каким должен быть объем выборки, чтобы те же границы для доли малообеспеченных жителей города гарантировать с надежностью 0,9973?

8. Как изменились бы результаты, если бы о доле малообеспеченных жителей вообще ничего не было бы известно?

9. Решить задачи 5 - 8, если население города неизвестно, но очень велико по сравнению с объемом выборки.