
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дисциплина «Научно-исследовательская работа студентов»
Дисциплина «Научно-исследовательская работа студентов»
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
Основными задачами статистической обработки результатов испытаний является определение среднего значения рассматриваемого параметра и оценка точности его вычисления. На практике значения генеральных характеристик оценивают по выборочным (эмпирическим) характеристикам с учетом нормального закона распределения ошибок.
Выборочное среднее значение 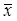 вычисляется по формуле
вычисляется по формуле
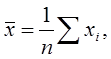
| (1) |
где xi - значение измеряемой величины для i-того образца;
п— число испытанных образцов (объем выборки).
Для оценки случайной ошибки измерений наиболее часто используют величину выборочного среднеквадратичного отклонения или среднеквадратичной ошибки (стандарт измерений):
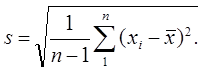
| (2) |
Выборочные числовые характеристики дают хорошие количественные оценки генеральных характеристик лишь при большом объеме выборок. При ограниченных объемах испытаний необходимо указать степень точности и надежности таких оценок.
Обозначим через α вероятность того, что величина 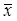 отличается от истинного значения хi на величину, меньшую, чем ∆х, т. е.
отличается от истинного значения хi на величину, меньшую, чем ∆х, т. е.
Р ( 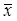 — ∆х < хi < — ∆х < хi < 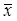 + ∆х)= α. + ∆х)= α.
| (3) |
Вероятность а называется доверительной вероятностью, а интервалы значений случайной величины хi от 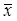 -∆х до
-∆х до 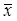 + ∆х называются доверительными интервалами.
+ ∆х называются доверительными интервалами.
При механических испытаниях доверительная вероятность обычно составляет 0,9 или 0,95.
Ширина доверительного интервала ∆х определяется числом измерений п и выборочными значениями 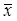 , s и вычисляется по следующей формуле:
, s и вычисляется по следующей формуле:
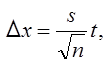
| (4) |
где t - коэффициент Стьюдента, величина которого зависит от объема выборки п и заданной доверительной вероятности α (табл. 1).
Совместно решая уравнения (3) и (4), получаем:
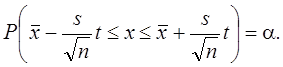
| (5) |
Таким образом,твердость при доверительной вероятности α находится в пределах
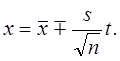
| (6) |
Из анализа функции нормального распределения следует, что среднеквадратическая выборочная ошибка ∆х=±1S наблюдается в 68% случаев, при ∆х=±2S – 95%, а при ∆х=±3S – 99,7%.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|