Хелпикс

Главная

Контакты

Случайная статья



Вывод.. Задача 1.1.2. Решение

⇐ ПредыдущаяСтр 2 из 2


Вывод.

 

 

 

Задача 1.1.2

Даны результаты восьми измерений ширины головки рельса:

 

               

 

Требуется:

1. Выполнить проверку наличия грубых погрешностей в представленной выборке из восьми измерений.

2. Выполнить интервальную оценку результатов измерений при доверительной вероятности Р = 0,90.

Решение

1. Проанализировав результаты восьми измерений значение

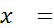                     ставим под сомнение.

2. Определим среднее арифметическое  значение измеренной величины (без учета сомнительного результата         ):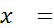

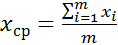, m=n-1=8-1=7

3. При числе измерений n < 20 среднее квадратическое отклонение (СКО) определяется по формуле:

 

 

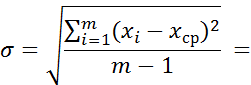
4. Произведем оценку результата измерения 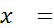        по критерию Романовского:

· уровень значимости =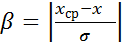

· допустимое значение критерия при m = 7 и вероятности 0,1

· βτ =       .

Так как β =         > βт =       , то результат 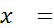                является грубой погрешностью («промахом»).

5. Произведем оценку результата измерения по критерию Шовинэ:

· отклонение результата измерения 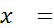         от среднего арифметического значения составляет

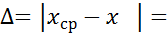
· допускаемое значение отклонения [Δ] = f(n) находим:

 

 

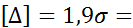
Так как Δ =   > [Δ] =          , то результат 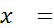   В является «промахом».

6. Доверительный интервал при доверительной вероятности Р = 0,90

   

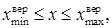
где

 

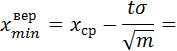
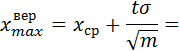
коэффициент Стьюдента t =       находится из таблицы .

 

 

Ответ:


 

Тема: «Экономическая эффективность стандартизации»

Задача 1.2. Для перевозки груза в железнодорожном контейнере УК-3 используется транспортный пакет с наружными расчетными размерами a, b и c.

Требуется:

1. Назначить геометрические размеры транспортного пакета для перевозки груза на основе рядов предпочтительных чисел: R5, R10, R20 и R40 (ГОСТ 8032-84).

2. Выбрать оптимальный (по экономическим показателям) вариант размещения транспортных пакетов в контейнере и выполнить схему их размещения в двух проекциях.

Исходные данные

A,мм B,мм C,мм а,мм b,мм c,мм
     

Решение

 

На основе рядов предпочтительных чисел 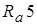, , 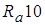 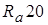и 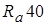 проведем обоснование геометрических размеров транспортного пакета для перевозки груза.

Ряд

Размеры пакета

Вариант размещения I

Вариант размещения II
a b c A/a B/b C/c Итого A/b B/a C/c Итого
Ra5                      
Ra10                      
Ra20                      
Ra40                      

При делении берем только целую часть числа. «Итого» получаем перемножением 3-х чисел в ряду.

Вывод.

Анализируя проведенные расчеты можно сделать вывод о том, что наиболее оптимальным по экономическим показателям является изготовление транспортного пакета для перевозки груза по размерам из ряда Ra =

 

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.