
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)»
(РУТ (МИИТ))
Кафедра: «Теоретическая и прикладная механика»
«Методы обработки и оценки результатов измерений»
«Экономическая эффективность стандартизации»
«Формы подтверждения соответствия»
КОНТРОЛЬНАЯ РАБОТА № 1
по дисциплине
«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ»
_________-_______-_________МСС.КР1.___.00.00.___.РР
___________________
(отметка о зачете)
Рецензент________________________ Студент_______________________
(Фамилия, И.О.) (Фамилия, И.О.)
__________________ «____»________20___г. Шифр ________________________

Москва 202
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
1.1. Задания по теме: «Методы обработки и оценки результатов измерений».
Задача 1.1.1.В результате работы пункта технического осмотра (ПТО) грузовых вагонов были получены выборки и выявлены вероятности появления дефектов ходовых частей, подчиняющиеся нормальному закону распределения. Выборки имеют различные показатели для смен, работающих в ночное и дневное время и характеризуются их средними арифметическими значениями 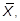 а также среднеквадратическими отклонениями σ. При этом накопленные данные для представленных выборок были получены за разное количество смен n.
а также среднеквадратическими отклонениями σ. При этом накопленные данные для представленных выборок были получены за разное количество смен n.
Требуется: Используя двухвыборочный t-критерий Стьюдента определить возможность статистического сравнения данных выборок и объединения их в одну общую выборку для получения обобщенных статистических данных за сутки.
 |
Исходные данные
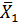 ,% ,%
| 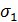 ,% ,%
| 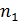
|  ,% ,%
| 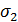 ,% ,%
| 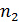
|
Решение
Двухвыборочный 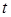 – критерий Стьюдента используется в случае, когда сравниваемые выборки подчиняются нормальному закону распределения и при этом обеспечивается условие равенства их дисперсий. Гипотеза о равенстве дисперсий в выборках проверяется сравнением частных несмещенных значений генеральной совокупности следующим образом:
– критерий Стьюдента используется в случае, когда сравниваемые выборки подчиняются нормальному закону распределения и при этом обеспечивается условие равенства их дисперсий. Гипотеза о равенстве дисперсий в выборках проверяется сравнением частных несмещенных значений генеральной совокупности следующим образом:
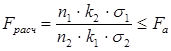 ,
,
где 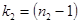 – степень свободы для значения в числителе;
– степень свободы для значения в числителе;
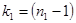 – степень свободы для значения в знаменателе;
– степень свободы для значения в знаменателе;
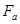 – критическая область значимости для исследуемого распределения.
– критическая область значимости для исследуемого распределения.
В нашем случае для 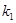 = и
= и 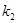 =
=
По таблице 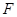 – распределения (прил. 3) найдем значение
– распределения (прил. 3) найдем значение
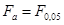 = .
= .
Следовательно, 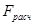 =
=
 Условие
Условие 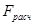 <
< 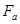 соблюдается, что свидетельствует о том, что существенной разницы между дисперсиями в исследуемых выборках нет
соблюдается, что свидетельствует о том, что существенной разницы между дисперсиями в исследуемых выборках нет  и их можно сравнить, используя двухвыборочный
и их можно сравнить, используя двухвыборочный 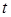 – критерий Стьюдента.
– критерий Стьюдента.
Нахождение 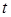 – критерия является наиболее часто используемым методом обнаружения сходства между средними значениями двух выборок. Значение данного критерия находится из условия:
– критерия является наиболее часто используемым методом обнаружения сходства между средними значениями двух выборок. Значение данного критерия находится из условия:
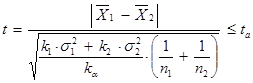 ,
,
где 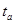 – сравнительный показатель, который зависит от уровня значимости
– сравнительный показатель, который зависит от уровня значимости 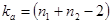 и находится из прил. 2.
и находится из прил. 2.
Подставляя данные, находим:
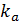 =
=
Из прил. 2 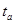 =
= 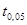 =
=
Значение 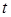 – критерий Стьюдента:
– критерий Стьюдента:
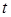 =
=
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|