
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Виды степенных средних
Виды степенных средних
| Показа-тель степени |
Вид
средней
Условия применения
Формула средней



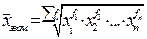
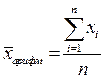
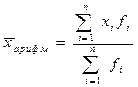
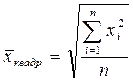
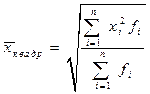
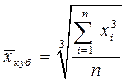
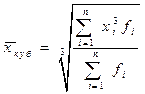
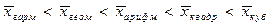
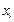 , наиболее часто повторяющееся, т.е. с наибольшей частотой.
, наиболее часто повторяющееся, т.е. с наибольшей частотой.
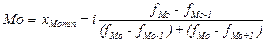 ,
где
,
где
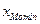 - нижняя граница модального интервала;
- нижняя граница модального интервала;
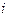 - длина модального интервала;
- длина модального интервала;
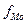 - частота модального интервала;
- частота модального интервала;
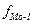 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
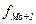 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
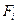 .
2. Определяем медианный интервал как тот, в котором накопленная численность единиц совокупности составляет более половины от их общего числа.
3. Используем формулу:
.
2. Определяем медианный интервал как тот, в котором накопленная численность единиц совокупности составляет более половины от их общего числа.
3. Используем формулу:
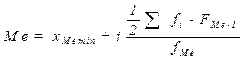 ,
где
,
где
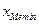 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
 - частота медианного интервала;
- частота медианного интервала;
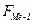 - накопленная частота интервала, предшествующего медианному.
- накопленная частота интервала, предшествующего медианному.