Задание №3. Задание №4. Задание №5. Задание №6. Задание №7. Домашнее задание. ВНИМАНИЕ!!!

⇐ ПредыдущаяСтр 2 из 2

Задание №3

АВСА1В1С1– правильная треугольная призма, AB=⁴√3, AA1=27. Найдите площадь полной поверхности призмы.

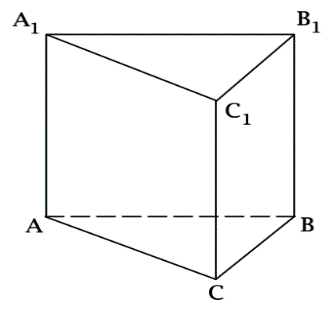Площадь равностороннего треугольника со стороной a равна a²√3/4, тогда

S_ABC=SA₁B₁C₁=(⁴√3)²√3/4=√3⋅√3/4=3/4,

S_AA1C1C=S_CC1B1B=S_AA1B1B=AA1⋅AB= ⁴√27⋅⁴√3 = ⁴√81=3. Таким образом, S_пов-ти _ABCA1B1C1 = 2⋅3/4+3⋅3=10,5.

Ответ: 10,5

Задание №4

В прямоугольной треугольной призме все боковые грани являются квадратами со стороной 103. Найдите объем призмы.

У квадрата все стороны равны ⇒ в основаниях призмы лежат равносторонние треугольники со сторонами, равными 10√3.

Тогда площадь основания: о с н Sосн.=1/2⋅10√3⋅10√3⋅sin60= =1/2⋅10√3⋅10√3⋅√3/2=75√3. Высота призмы равна

Рис.4 стороне квадрата, тогда объем призмы: 10√3⋅75√3=2250.

Ответ: 2250

Задание №5

Дана правильная треугольная призма. Площадь основания равна площади одной из боковых граней и равна 4√3. Найдите объем призмы.

Рис.4

Так как призма является правильной, то в основаниях призмы лежат равносторонние треугольники, поэтому все боковые грани равны друг другу и являются прямоугольниками. Обозначим высоту призмы за h, а сторону правильного треугольника за x. Тогда найдем площадь основания: Sосн.=1/2⋅x²⋅sin60=1/2⋅x²⋅√3/2=√3/4⋅x²=4√3 ⇒ x²=16 ⇒ x=4. Высоту выразим из формулы для площади боковой грани: S=4√3=x⋅h=4⋅h ⇒ h=√3. Наконец, найдем объем призмы: V=h⋅Sосн.= √3⋅4√3=12.

Ответ: 12

Задание №6

В правильной четырехугольной призме ABCDA1B1C1D1 известно, что DB1=2CD. Найдите угол между диагоналями AC1 и B1D. Ответ дайте в градусах.

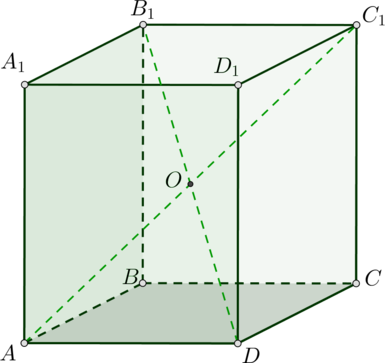Так как призма четырехугольная и правильная, то в основании лежит квадрат и она прямая. Следовательно, AD=CD и DB1=2AD. Диагонали призмы пересекаются и точкой пересечения O делятся пополам, следовательно, OD=1/2DB1=AD. Так как призма правильная, то диагонали равны, значит, AO=OD=AD. Следовательно, △AOD правильный и ∠AOD=60˚. Это и есть угол между DB1 и AC1. Ответ: 60˚

Задание №7

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми AA1 и CB1. Ответ дайте в градусах.

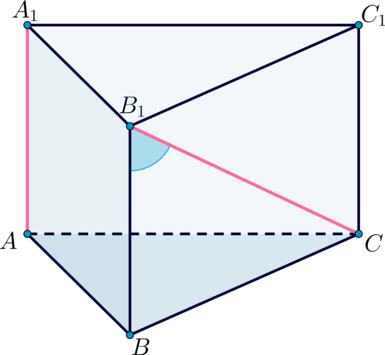Для того, чтобы найти угол между прямыми, не лежащими в одной плоскости, нужно одну из прямых параллельно перенести в плоскость, в которой лежит вторая прямая. Заметим, что BB1∥AA1. Следовательно, угол между AA1 и CB1 равен углу между прямыми BB1 и CB1. Так как все ребра призмы равны, то грань BCC1B1 представляет собой квадрат, где CB1 – диагональ. Следовательно, ∠BB1C=45˚. Ответ: 45˚

Домашнее задание

1) В правильной четырехугольной призме S_б=32 см², S_полн = 40см². Найти высоту призмы

2) Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

Критерии оценивания:

1. Оценка «отлично»- выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.

2. Оценка «хорошо»- выставляется обучающемуся, если допущены незначительные погрешности в задании.

3. Оценка «удовлетворительно»- выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.

4. Оценка «неудовлетворительно»- выставляется обучающемуся, если задания не решены.

ВНИМАНИЕ!!!

Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev

Преподаватель: Коломиец Светлана Григорьевна

⇐ Предыдущая 12