Тема: 1. Правильная призма. Решение задач.

Тема: 1. Правильная призма. Решение задач.

Дата: 05.11.2020 г.

Группа: ПЦ-262

Студенты должны знать: понятие призмы, виды призм, понятие площади поверхности призмы, формулы для вычисления площади полной и боковой поверхности прямой призмы.

Студенты должны уметь:применять в задачах понятия призмы, площади поверхности призмы.

1. Актуализация опорных знаний

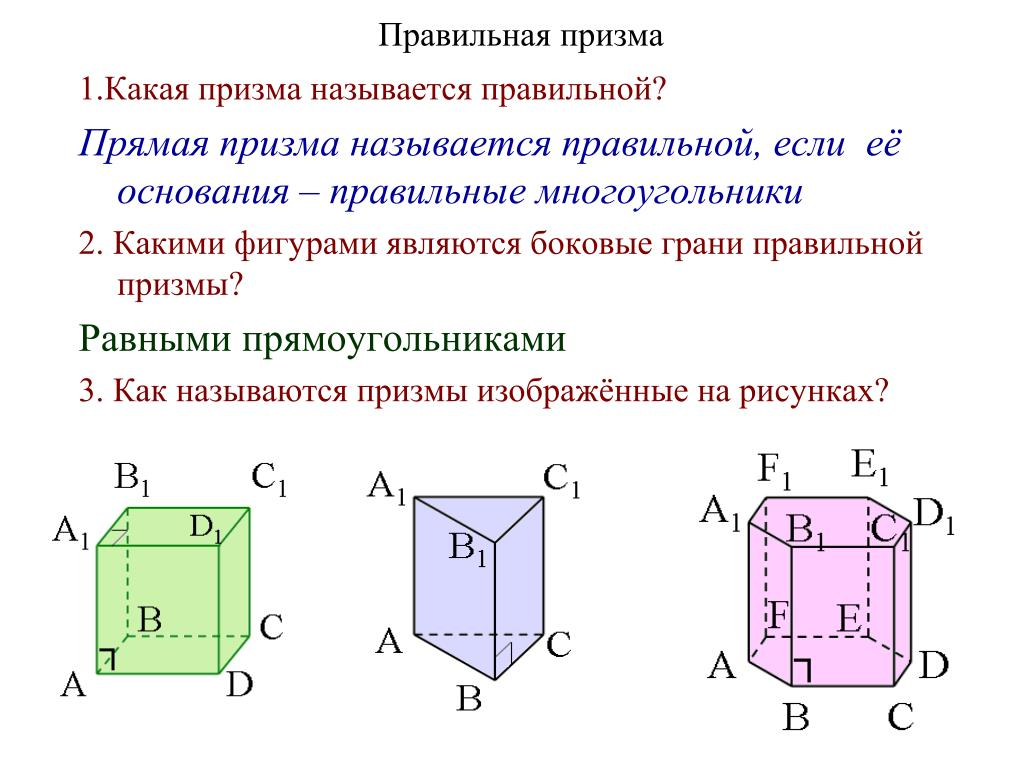
2.Решение задач

Дана правильная четырехугольная призма, диагональ которой равна 15, а диагональ основания равна 10√2. Найдите площадь полной поверхности призмы.

Задание №1

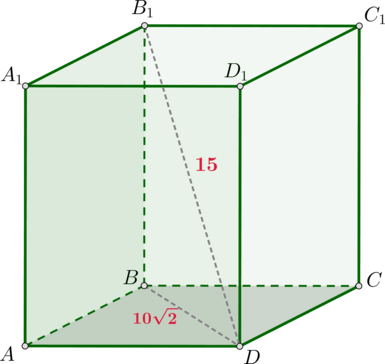Пусть ABCDA1B1C1D1 – данная призма. Так как она правильная, то в основании лежит квадрат и она является прямой. Тогда △BB1D прямоугольный, следовательно, по теореме Пифагора BB1=√15²−(10√2)² = 5. Так как диагональ квадрата в √2 раз больше его стороны, то AB=BD/√2=10. Следовательно,

Следовательно, S_пов-ти =2S_ABCD+4S_AA1D1D=2⋅10²+4⋅10⋅5=400.

Ответ: 400

Задание №2

Дана прямая призма, в основании которой лежит равнобедренная описанная около окружности трапеция ABCD с боковой стороной, равной 5, и высотой, равной 3. Боковое ребро призмы равно 2. Найдите площадь полной поверхности призмы.

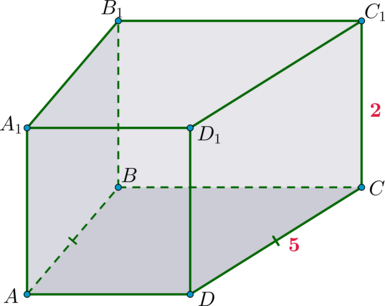Пусть AB=CD=5. Так как трапеция описанная, то суммы противоположных сторон равны, следовательно, AD+BC=AB+CD=10. Следовательно, ее площадь равна SABCD=(AD+BC)/2⋅h=10/2⋅3=15.

Площадь боковой поверхности призмы равна S′=(AB+BC+CD+AD)⋅AA₁=(10+10)⋅2=40.

Следовательно, площадь полной поверхности равна

S_пов-ти = 40+15+15=70.

Ответ: 70

12 Следующая ⇒