
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Ряды
Тема: Ряды
Ряд представляет собой сумму членов бесконечной последовательности. Ряды бывают числовые и функциональные – когда суммируются числа либо функции соответственно.
Функциональные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, пределов функций, определенных интегралов, находят приближенные решения дифференциальных уравнений.
Так, многие определенные интегралы, получающиеся при решение практических задач, не могут быть вычислены с помощью формулы Ньютона-Лейбница, поскольку применение этой формулы связано с нахождением первообразной, которая не всегда выражается в элементарных функциях.
Если, однако, подынтегральная функция разлагается в функциональный ряд, а отрезок интегрирования входит в область сходимости этого ряда, то возможно приближенное вычисление интеграла с любой заданной точностью.
Чтобы работать с функциональными рядами, нужно сначала разобраться с числовыми рядами, чем мы сейчас и займемся.
Шилкина, с. 95 – 97.
Выписать определения и формулы для следующих понятий:
на стр. 95 – ряд, член ряда, общий член ряда, частичная сумма, сумма ряда, сходящийся и расходящийся ряд;
на стр. 97 – геометрический ряд, гармонический ряд, обобщенный гармонический ряд (он же ряд Дирихле).
Пример 1.Написать 4 первых члена ряда, если задан его общий член
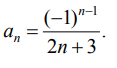

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|