
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи для решения. Тема 2 Правило Крамера
Задачи для решения
1 Решить системы линейных уравнений матричным методом
а) 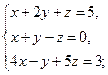 б)
б) 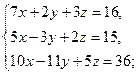 в)
в) 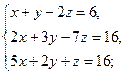
г)  д)
д)  е)
е) 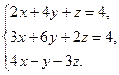
2 Решить системы линейных уравнений
а) 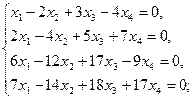 б)
б) 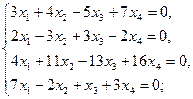
в) 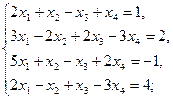 г)
г) 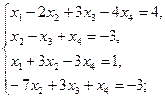
д) 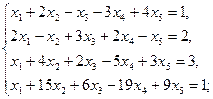 е)
е) 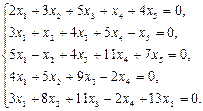
Тема 2 Правило Крамера
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
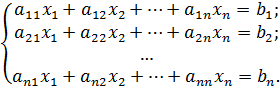
Обозначим через Δ и Δj определитель матрицы системы и определители, полученные из определителя Δ заменой j-го столбца столбцом свободных членов системы:
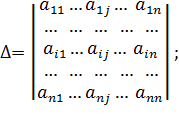
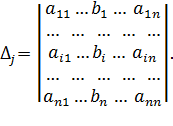
Если определитель матрицы системы отличен от нуля, Δ≠0, то решение системы определяется равенствами:
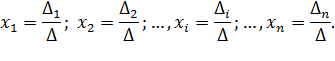
Пример Решим по правилу Крамера систему трех линейных уравнений с тремя неизвестными.

Запишем матрицу системы, столбец свободных членов и вычислим определитель матрицы системы:
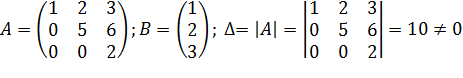 .
.
Определитель матрицы системы отличен от нуля. Система имеет единственное решение. Вычислим его по формулам Крамера. Для этого найдем определители 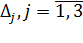 .
.
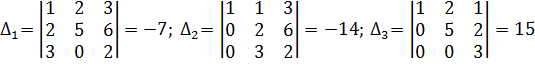 .
.
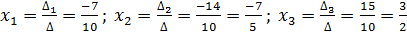 .
.
Проверим:
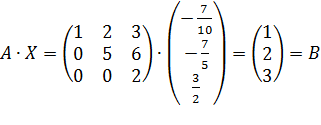 .
.
1 Решить систему линейных уравнений по правилу Крамера:
а) 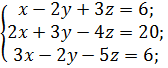 б)
б) 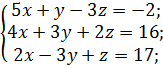 в)
в) 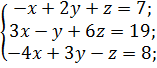
г) 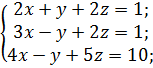 д)
д)  ж)
ж) 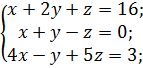
з)  и)
и) 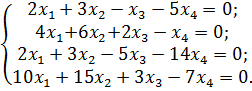
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|