
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 7. Ряды динамики в статистике
Тема 7. Ряды динамики в статистике
1. Классификация рядов и правила их построения
2. Показатели изменения уровней рядов динамики
3. Компоненты временных рядов
Видео по теме https://youtu.be/1HuvtZuTRp0
1. вопрос
Одной из важных задач статистики является изучение развития процессов и явлений во времени. Эта задача и решается с помощью построения рядов динамики.
Ряд динамики – это ряд расположенных в хронологическом порядке показателей, характеризующих изменение величины общественных явлений во времени. 
Правильно построенный динамический ряд состоит из сопоставимых статистических показателей. Для этого необходимо, чтобы состав изучаемой совокупности был один и тот же на всем протяжении ряда, т.е. относился к одной и той же территории, к одному и тому же кругу объектов. Кроме того, данные ряда должны быть выражены в одних и тех же единицах измерения, а промежутки времени между значениями ряда должны быть по возможности одинаковыми.
Виды рядов динамики:
В зависимости от того, к моментам или периодам времени привязываются статистические данные различают:
1. моментные ряды динамики- это когда уровни ряда динамики показывают состояние явления на определённый момент времени или на определенную дату.
Особенность моментного ряда динамики в том, что некоторые его уровни содержат элементы повторного счёта, т.е. каждый последующий уровень полностью или частично содержит в себе предыдущий уровень. Поэтому суммирование уровней моментного динамического ряда не имеет смысла, а имеет значение только разность уровней ряда.
Напр.: бессмысленно складывать численность работающих по состоянию на 1 января, 1 февраля, 1 марта и т. д. Полученная сумма ничего не выражает, т.к. в ней многократно повторяются одни и те же показатели.
2. интервальные ряды динамики - это когда уровни ряда динамики характеризуют размеры общественных явлений за определенные интервалы времени.
Уровни интервального ряда динамики могут быть суммированы.
В зависимости от вида статистических показателей ряды динамики подразделяются:
1. ряды динамики абсолютных величин. Они являются первоначальными, так как их получают при сводке материалов статистического наблюдения.
2. ряды динамики относительных величин. Такие ряды являются производными. Они характеризуют темпы динамики изучаемого явления, изменение его структуры интенсивности. Суммирование уровней в таких рядах не имеет смысла, а используется такие ряды для характеристики качественных изменений экономики.
3. ряды динамики средних величин. Это ряды показателей, которые выражают средние значения изучаемого явления за определенные промежутки времени. Суммирование уровней в таких рядах не имеет смысла, а используются такие ряды для характеристики качественных изменений экономики.
2. Вопрос
При изучении динамики социально-экономических явлений рассчитывают аналитические показатели:
-абсолютные приросты;
· темпы роста;
· темпы прироста;
· абсолютное значение одного процент прироста (снижения).
Рассчитываются эти показатели через абсолютное или относительное сравнение уровней динамического ряда.
Уровнем ряда называется абсолютная величина каждого члена динамического ряда. Различают:
· начальный уровень- это величина первого члена ряда - 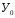
· конечный уровень - это величина последнего члена ряда - 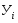
· средний уровень – это средняя из всех значений ряда - 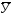
При этом сравниваемый уровень называется текущим, а тот уровень, а которым сравнивают - базисным.
Если сравнивается каждый последующий уровень с предыдущим, то получают цепные показатели динамики.
Если каждый уровень сравнивается с начальным, то получают базисные показатели динамики.
1.Абсолютный прирост –это разность двух уровней ряда динамики.
Он показывает, на сколько единиц данный уровень больше или меньше уровня, взятого для сравнения. Он выражается в тех же единицах, что и уровни ряда  динамики.
динамики. 
Цепной абсолютный прирост( 
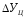 ) рассчитывается как разность
) рассчитывается как разность
между текущим уровнем ( 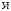 ) и уровнем, который ему предшествует (
) и уровнем, который ему предшествует ( 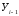 ):
): 

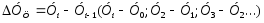
Базисный абсолютный прирост (  Уб )рассчитывается как разность между сравниваемым уровнем (
Уб )рассчитывается как разность между сравниваемым уровнем ( 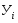 ) и уровнем принятым за базу сравнения (
) и уровнем принятым за базу сравнения ( 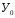 ):
):
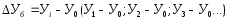
2.Темп роста – это отношение двух уровней ряда динамики.
Он показывает, во сколько раз больше или меньше или сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. Темп роста может выражаться в коэффициентах или в процентах.
Цепной темп роста (  )– это отношение между текущими уровнями
)– это отношение между текущими уровнями
(  ) и предшествующим (
) и предшествующим ( 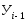 ):
):
Тц=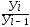
 (
(  ;
;  ;
; 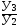 …)
…)
Базисный темп роста (  ) -это отношение базисного абсолютного
) -это отношение базисного абсолютного
прироста(Уi) к базисному уровню (У0):
Тб= 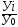 (
(  ;
;  ;
; 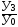 …)
…)
Если темп роста меньше единицы, то имеет место не рост, а снижение анализируемого уровня.
3. Темп прироста- это отношение абсолютного прироста к уровню, принятому за базу сравнения.
Он показывает на сколько процентов уровень данного периода больше или меньше уровня, принятого за базу сравнения. Может выражаться в коэффициентах.
Цепной темп прироста (∆Тц ) - это отношение цепного абсолютного
прироста (∆ Уц к предыдущему уровню (Уi-1 ):
∆Тц=  или ΔТц =Тц-1
или ΔТц =Тц-1
Базисный темп прироста (∆ТБ) – это отношение базисного абсолютного прироста (∆ УБ ) к базисному уровню (У0 ) :
∆ТБ= 
Темп прироста может быть, как положительный, так и отрицательной величиной.
4. Абсолютное значение одного процента прироста (А)- это отношение абсолютного прироста за определенный период к темпу прироста за этот же период, выраженному в процентах.
Этот показатель раскрывает, какая абсолютная величина скрывается за один процент прироста:
А= 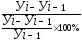 или А= 0,01
или А= 0,01 
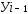
Выражается абсолютное значение одного процента прироста или снижения в тех же единицах измерения, что ианализируемый уровень динамического ряда.
Между многими аналитическими показателями существует определенная взаимосвязь:
1. Сумма цепных абсолютных приростов за какой-то период времени, равна базисному абсолютному приросту за весь этот период:
∆ У= ∑ ∆ УЦ = Уn- У0
2. Разность между анализируемыми и предыдущим базисными абсолютными приростами даёт соответствующий цепной абсолютный прирост:
(Уi-У0)- (Уi-1 -У0)= Уi- Уi-1
3. Последовательное произведение цепных темпов роста, выраженных в коэффициентах за определенный период времени даёт базисный темп роста за этот же период:

4. Отношение анализируемого базисного темпа к предыдущему даёт соответствующий цепной темп роста:
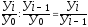
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|