Контакты

Случайная статья

Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Задача

Является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:

; .

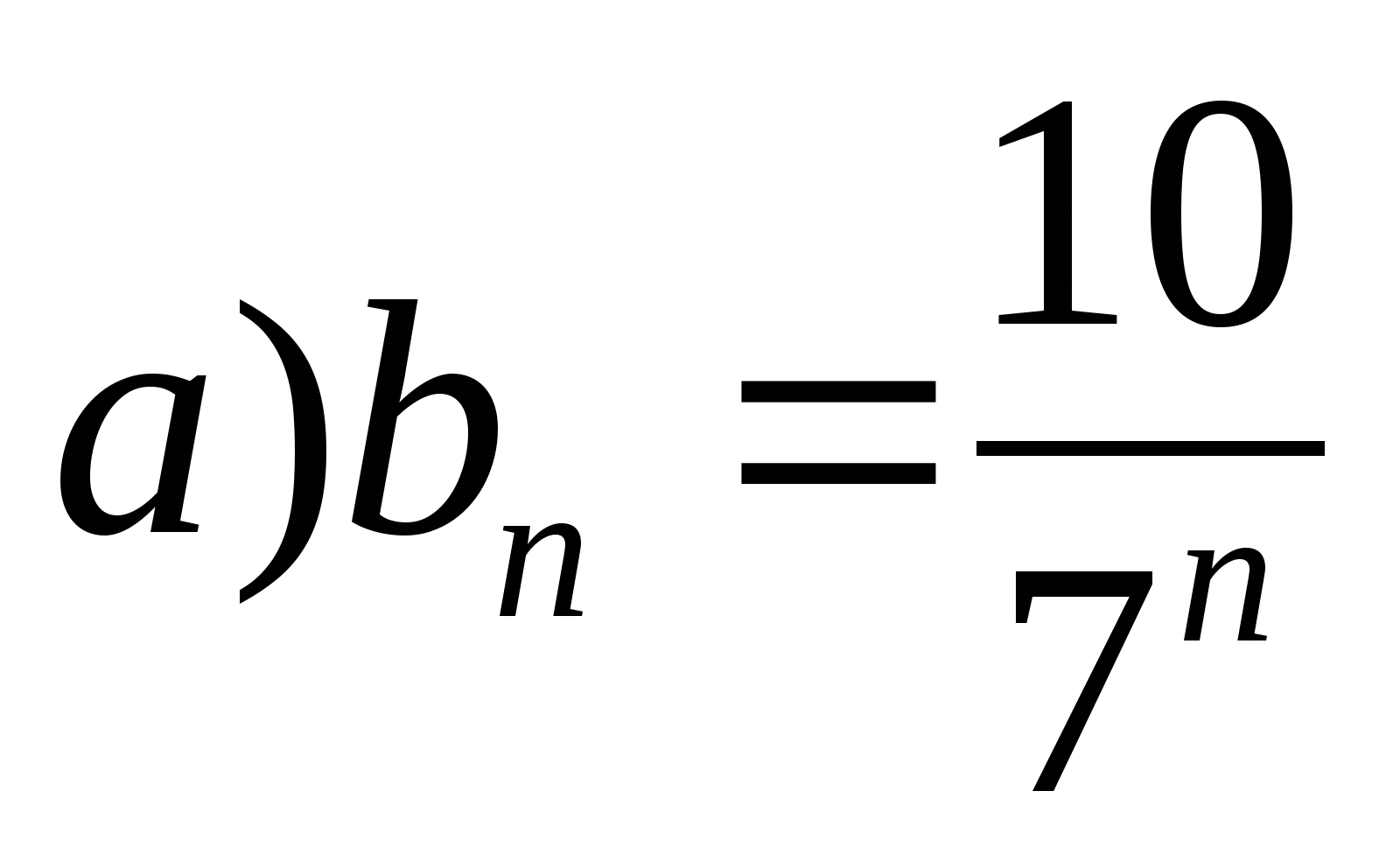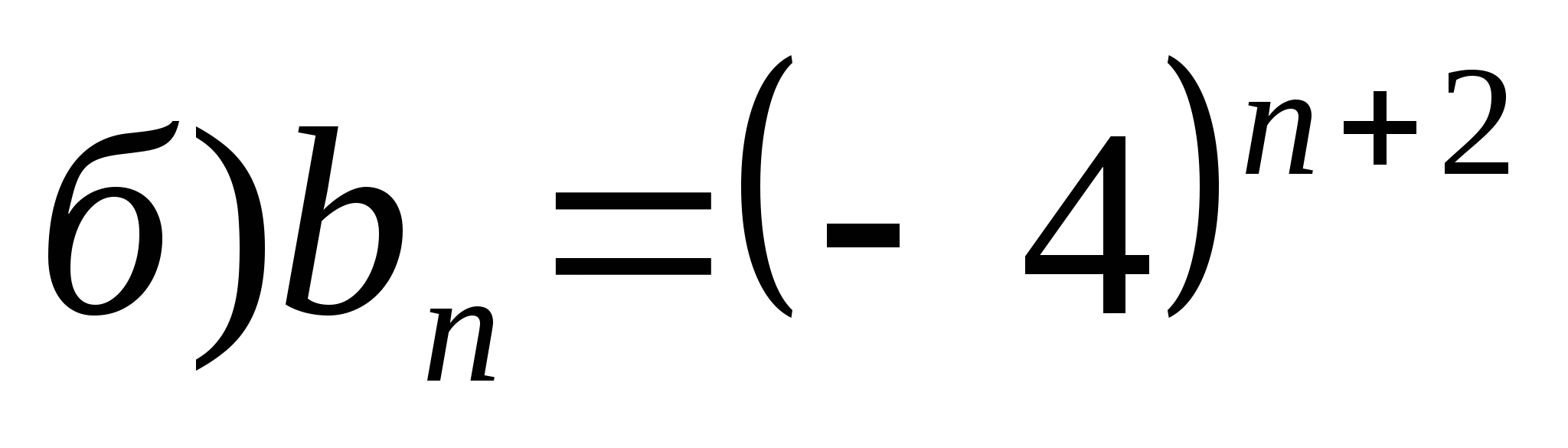Решение:

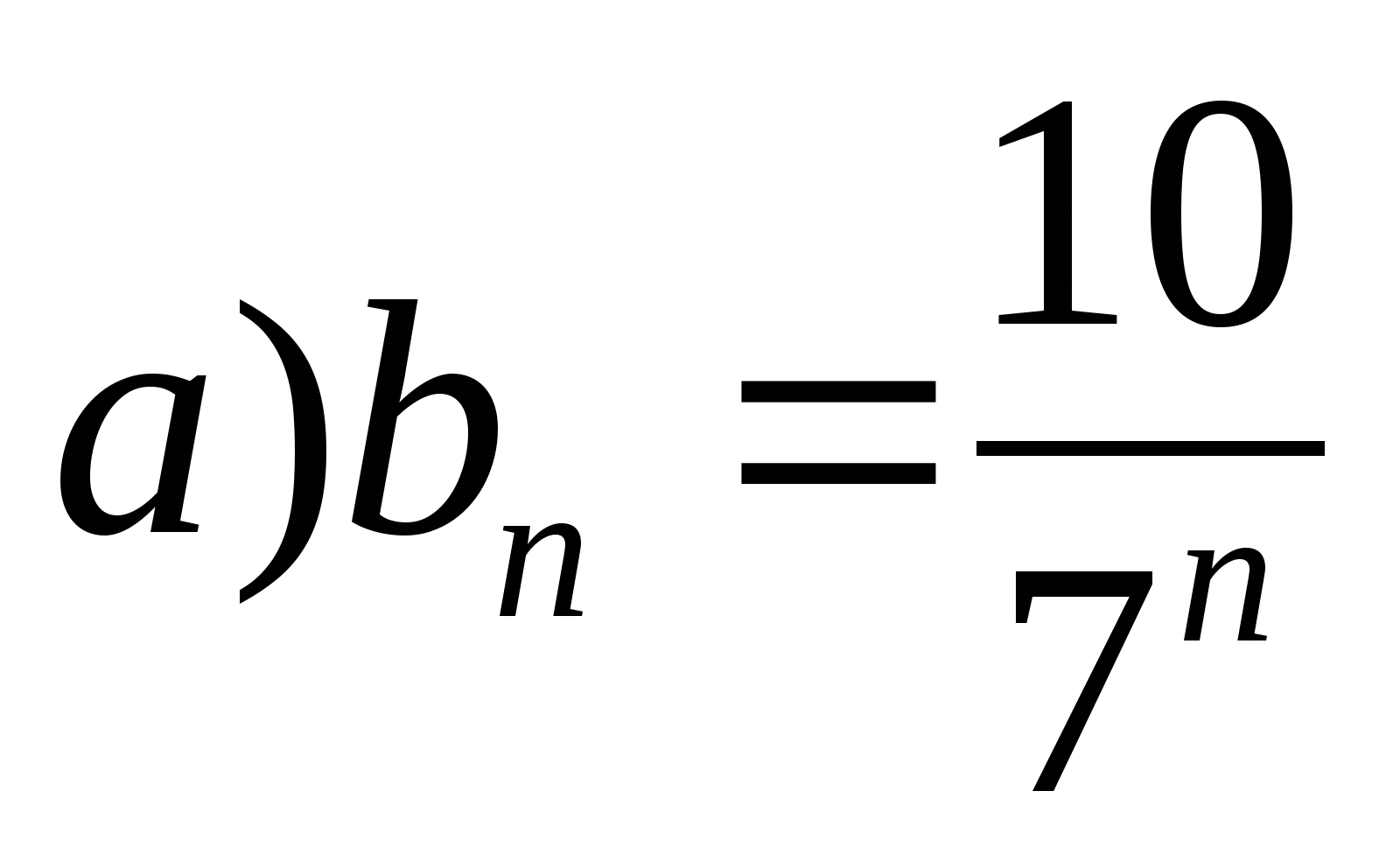. Найдем q.

; ; ; .

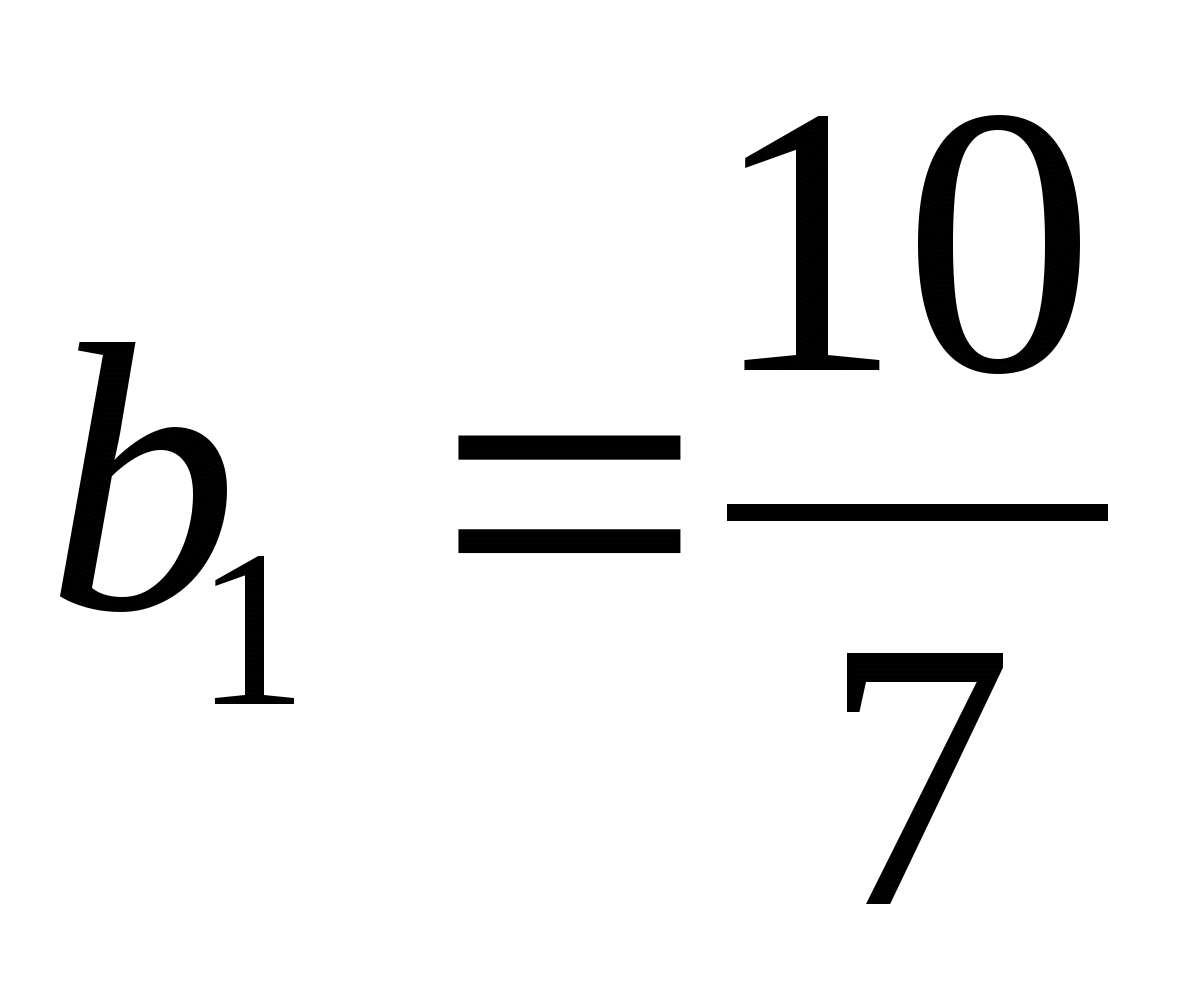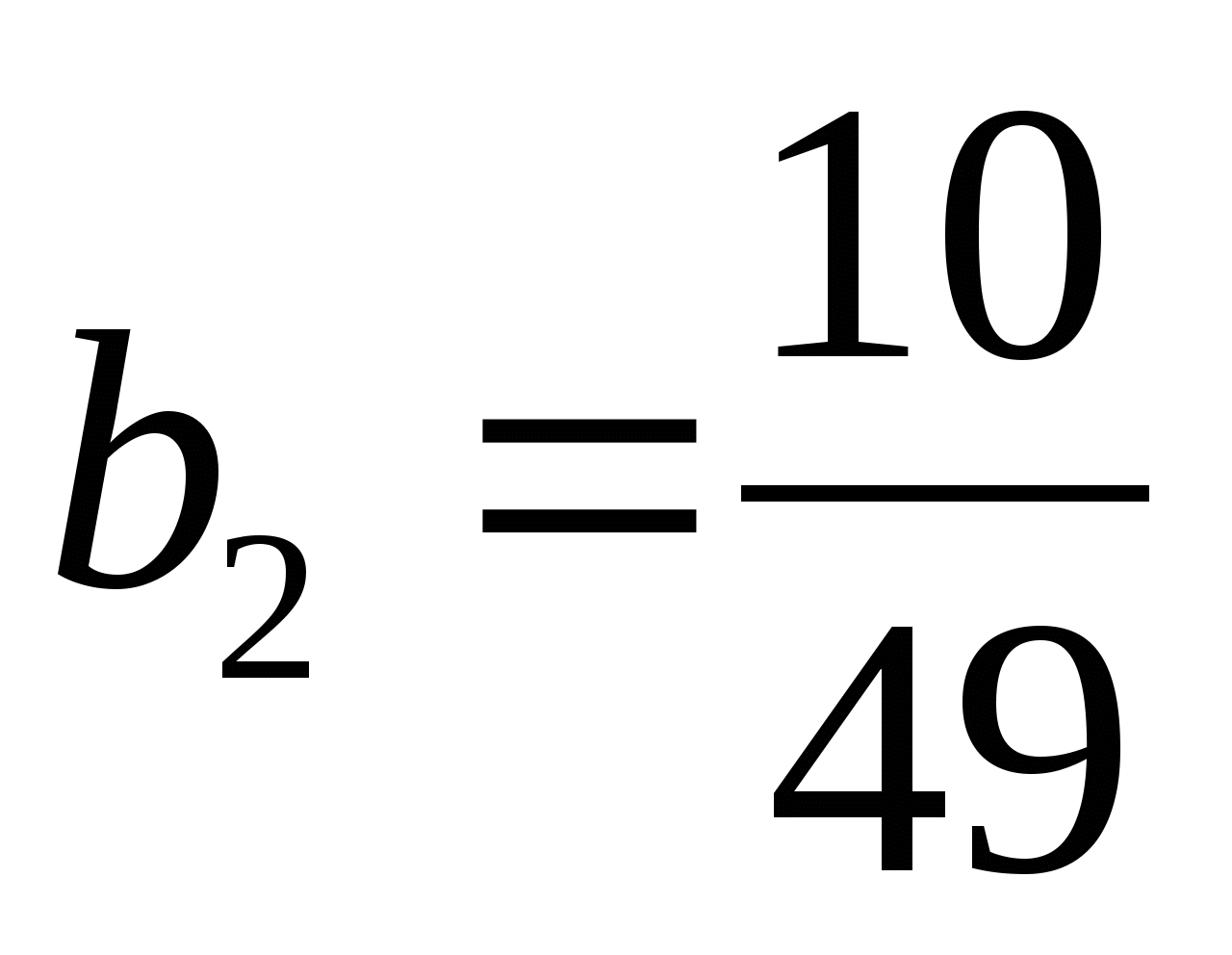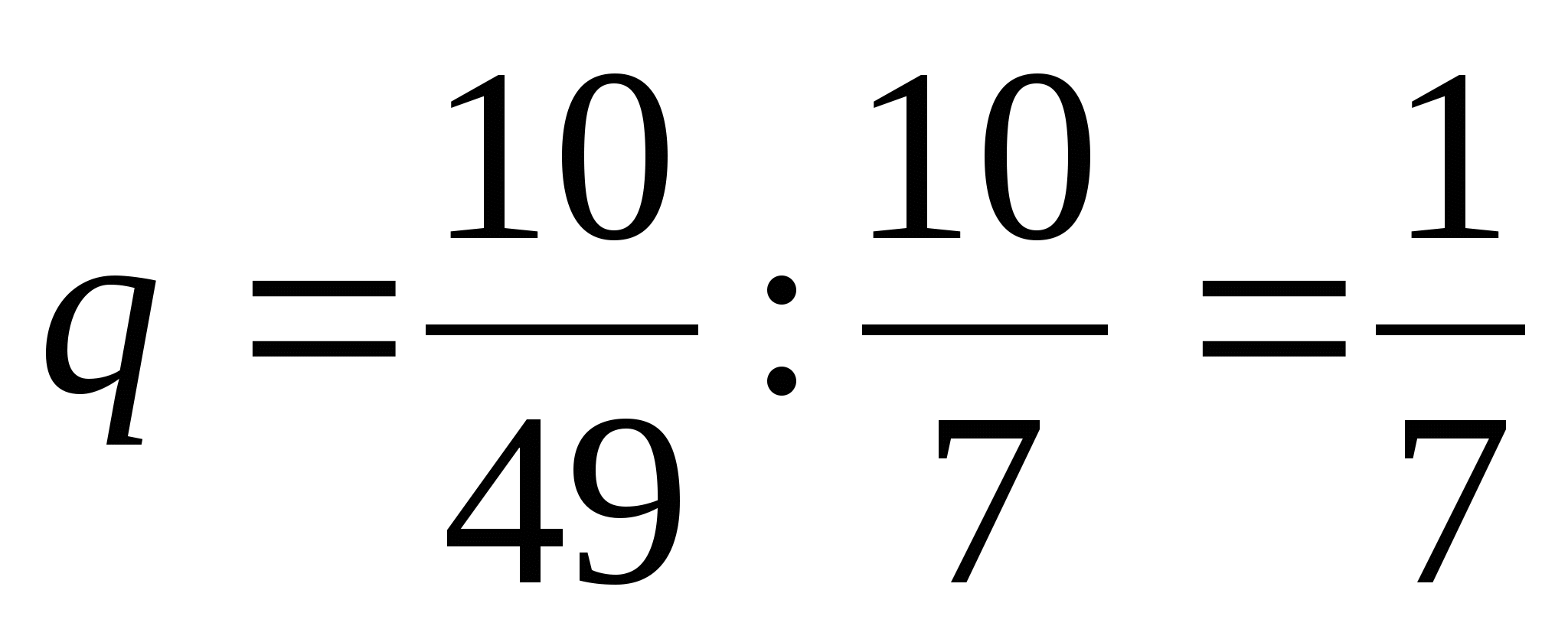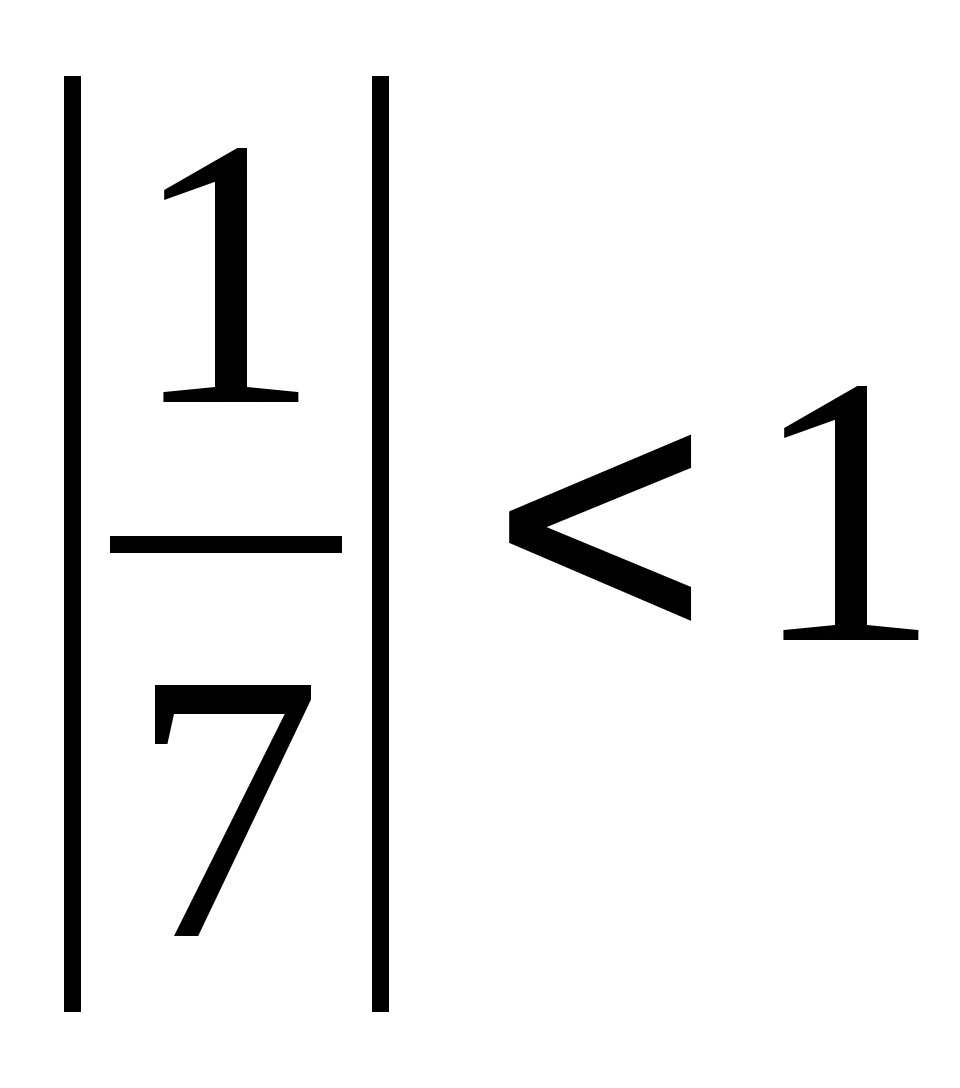данная геометрическая прогрессия является бесконечно убывающей.

б) данная последовательность не является бесконечно убывающей геометрической прогрессией.

Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: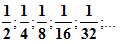

Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.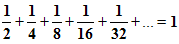

Но в левой части этого равенства – сумма бесконечного числа слагаемых.

Рассмотрим сумму n первых слагаемых.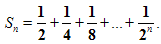

По формуле суммы n первых членов геометрической прогрессии, она равна .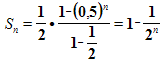

Если n неограниченно возрастает, то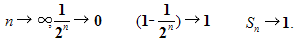

или 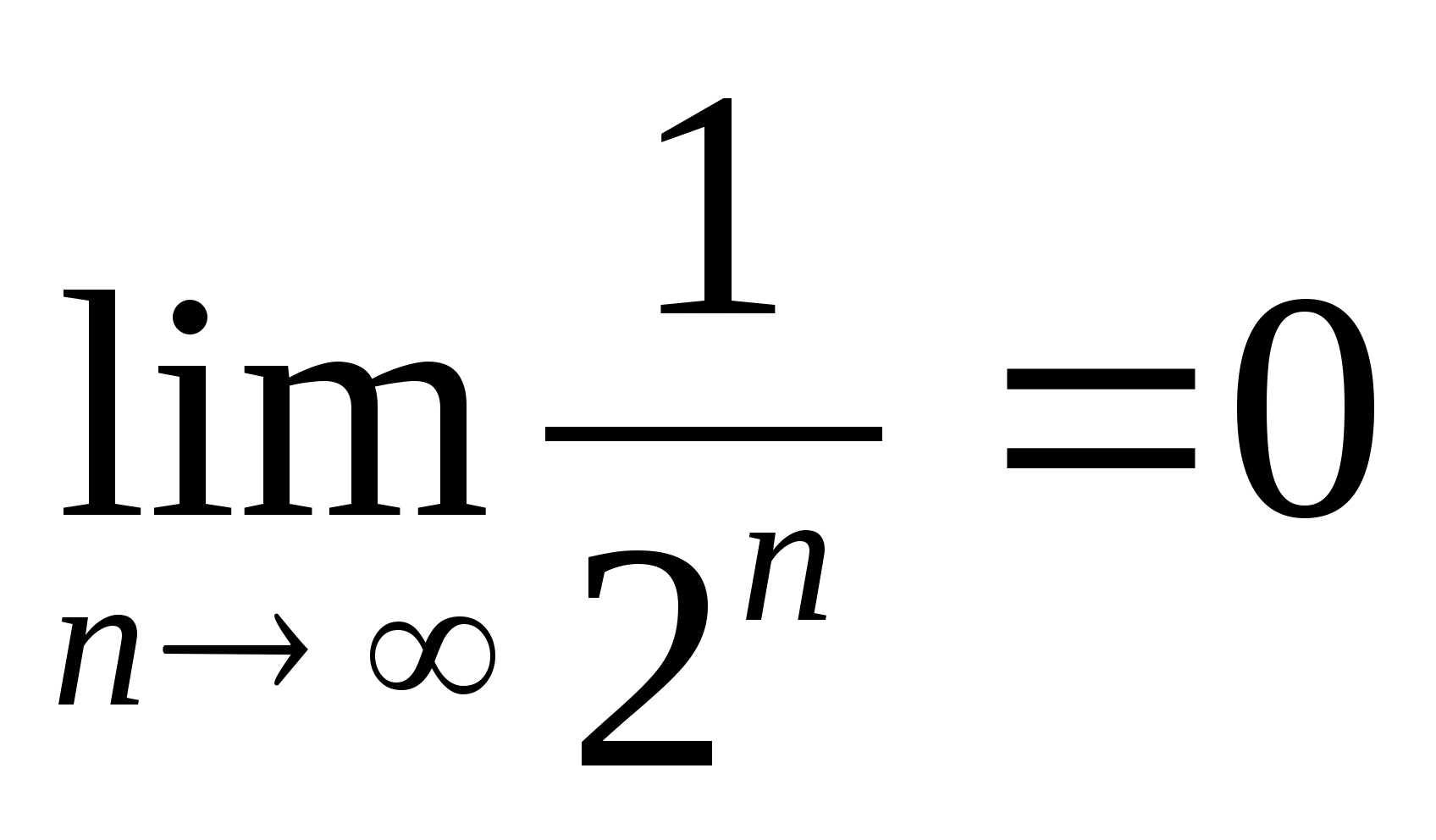. Поэтому 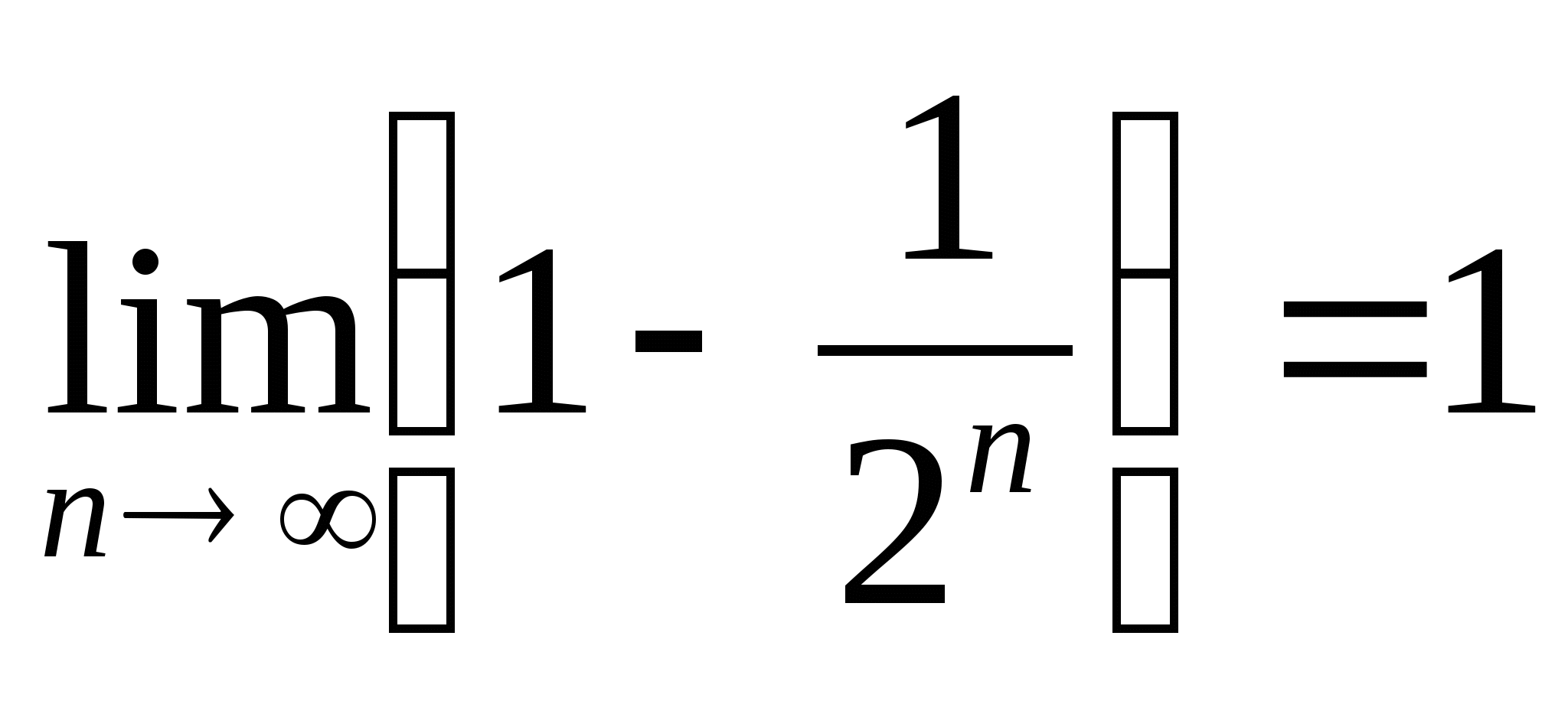, т.е. .

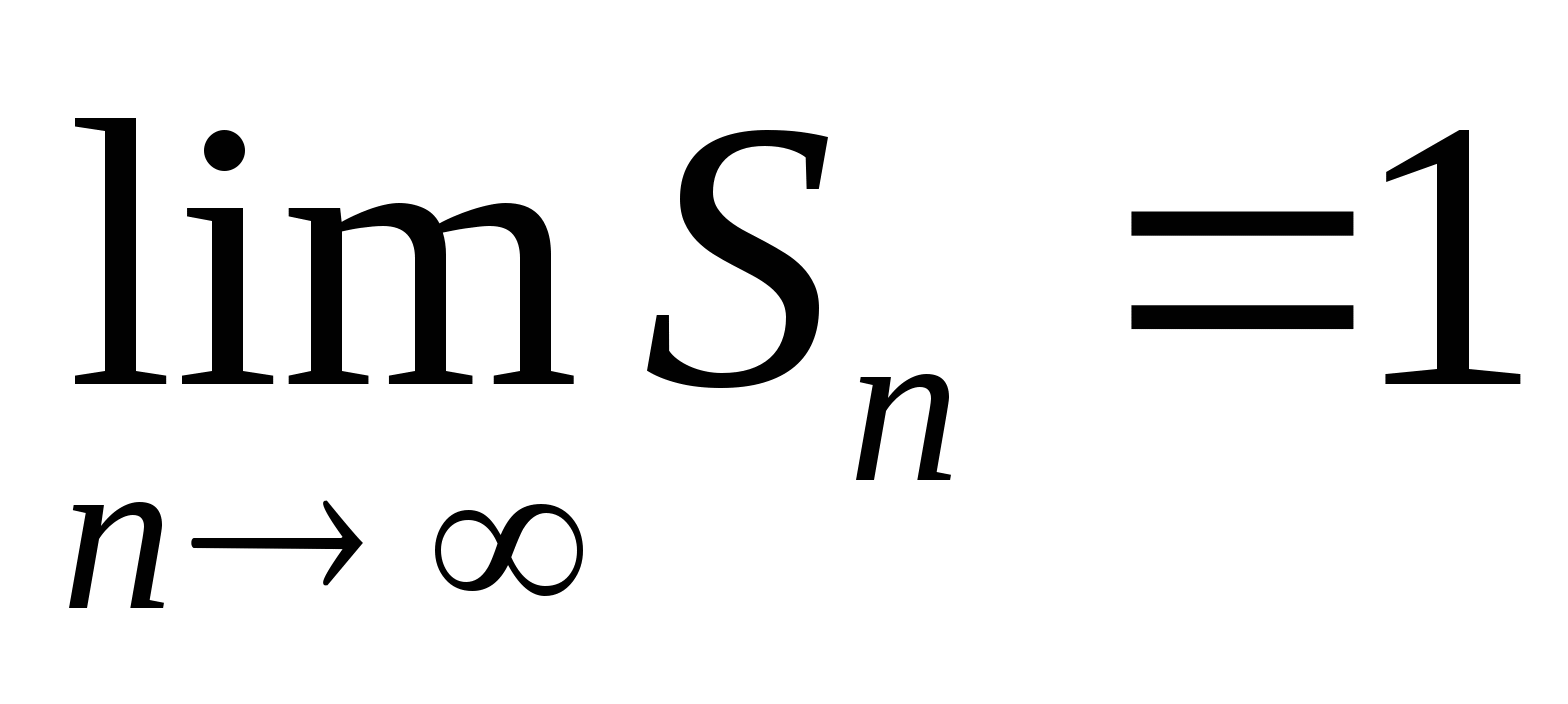Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .

Например, для прогрессии ,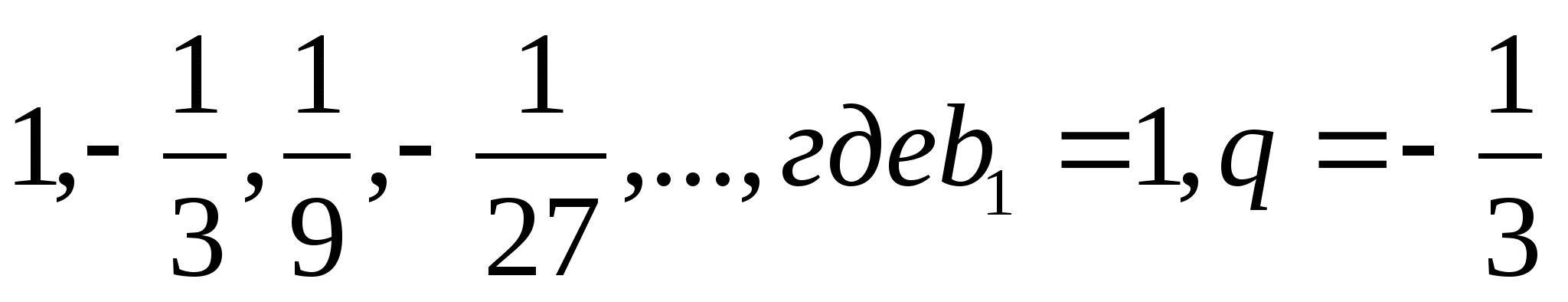

имеем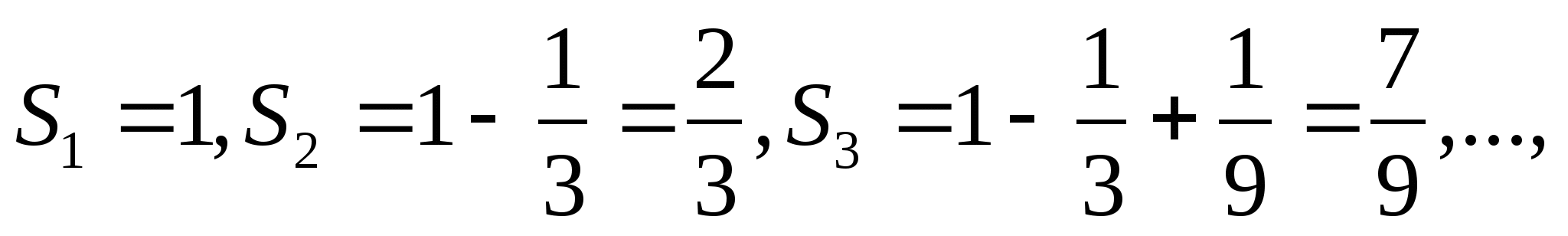

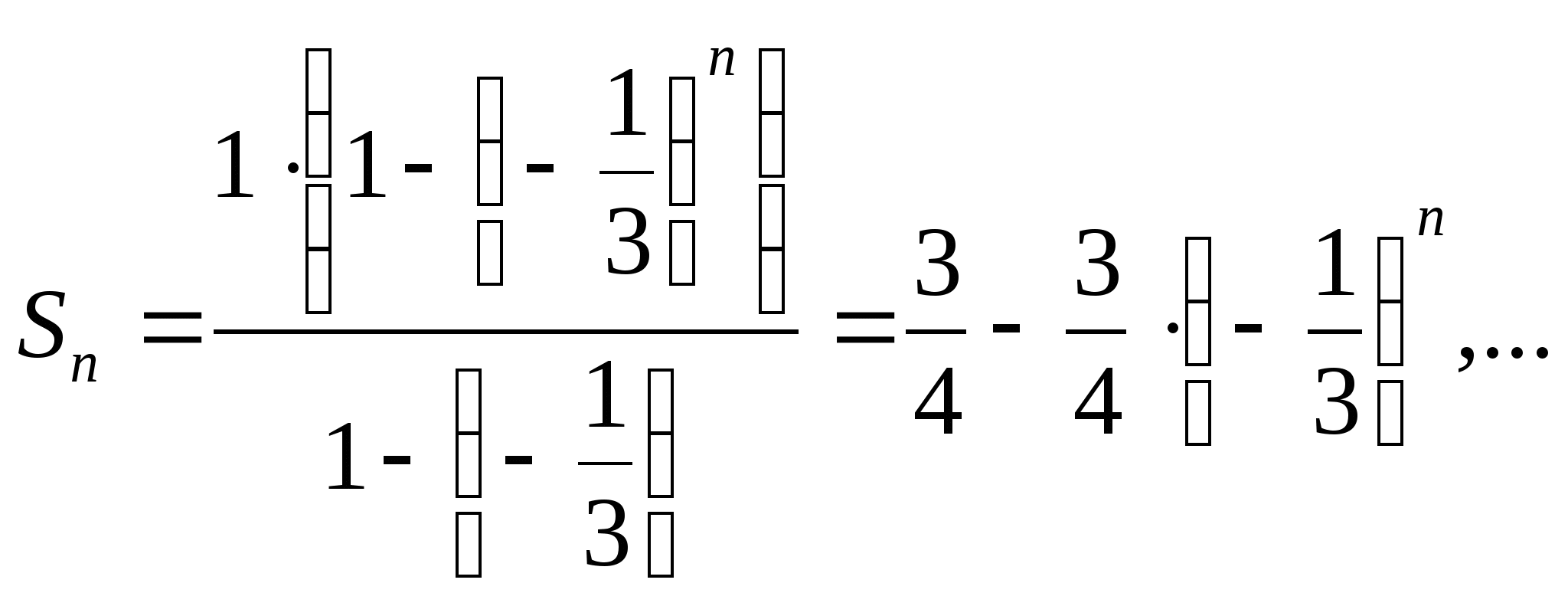Так как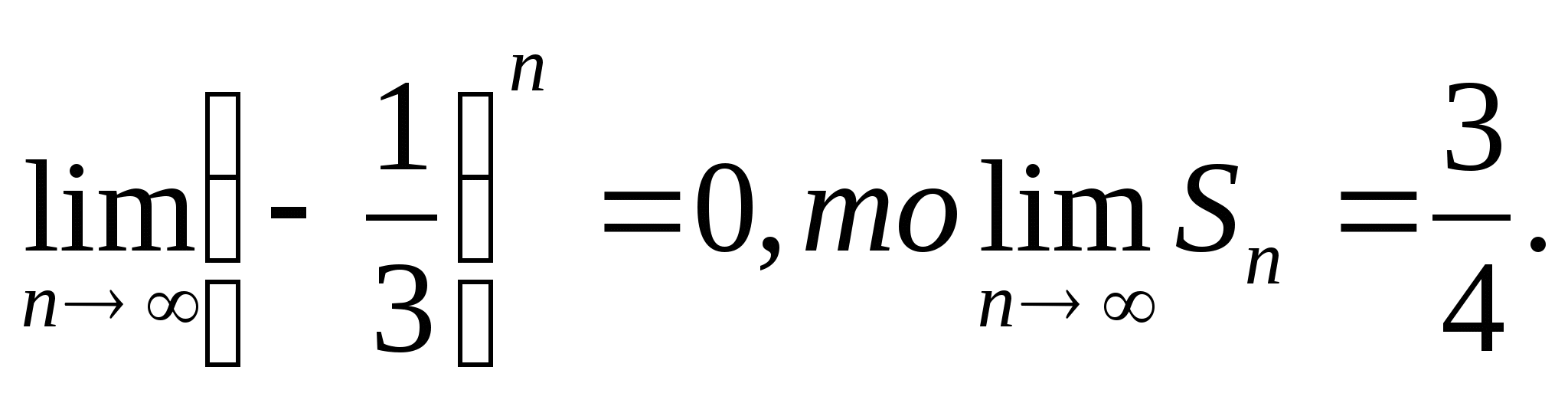

Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле .

III. Осмысление и закрепление(выполнение заданий).№4.38

IV. Подведение итогов.

Ø С какой последовательностью сегодня познакомились?

Ø Дайте определение бесконечно убывающей геометрической прогрессии.

Ø Как доказать, что геометрическая прогрессия является бесконечно убывающей?

Ø Назовите формулу суммы бесконечно убывающей геометрической прогрессии.

⇐ Предыдущая 123 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.