Тема: Бесконечно убывающая геометрическая прогрессия

Стр 1 из 3Следующая ⇒

Тема: Бесконечно убывающая геометрическая прогрессия

Дата: 02.11.2020 г.

Группа: ПЦ-265

Цель урока: ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией.

Студенты должны знать: понятие бесконечной убывающей геометрической прогрессии.

Студенты должны уметь: применять на практике в заданиях понятия бесконечно убывающей геометрической прогрессии.

1.Актуализация опорных знаний

2.Разминка. Решение упражнений на повторение.

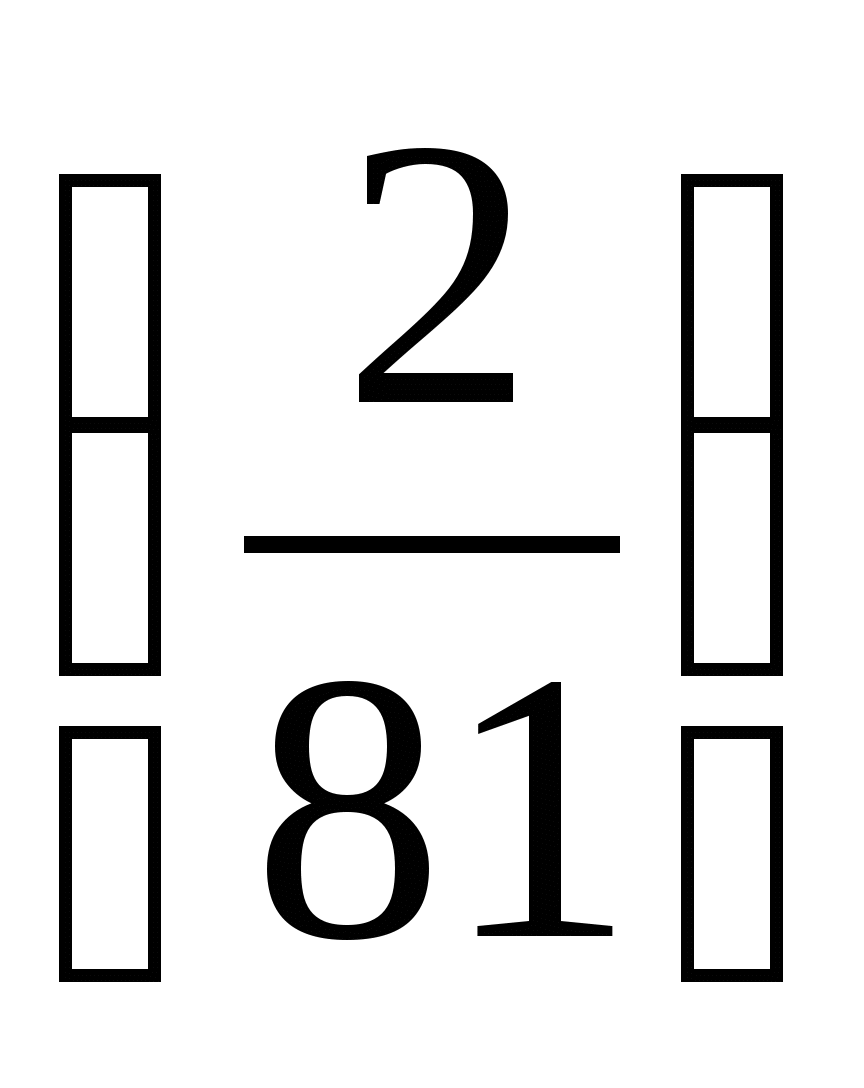1. Для геометрической прогрессии 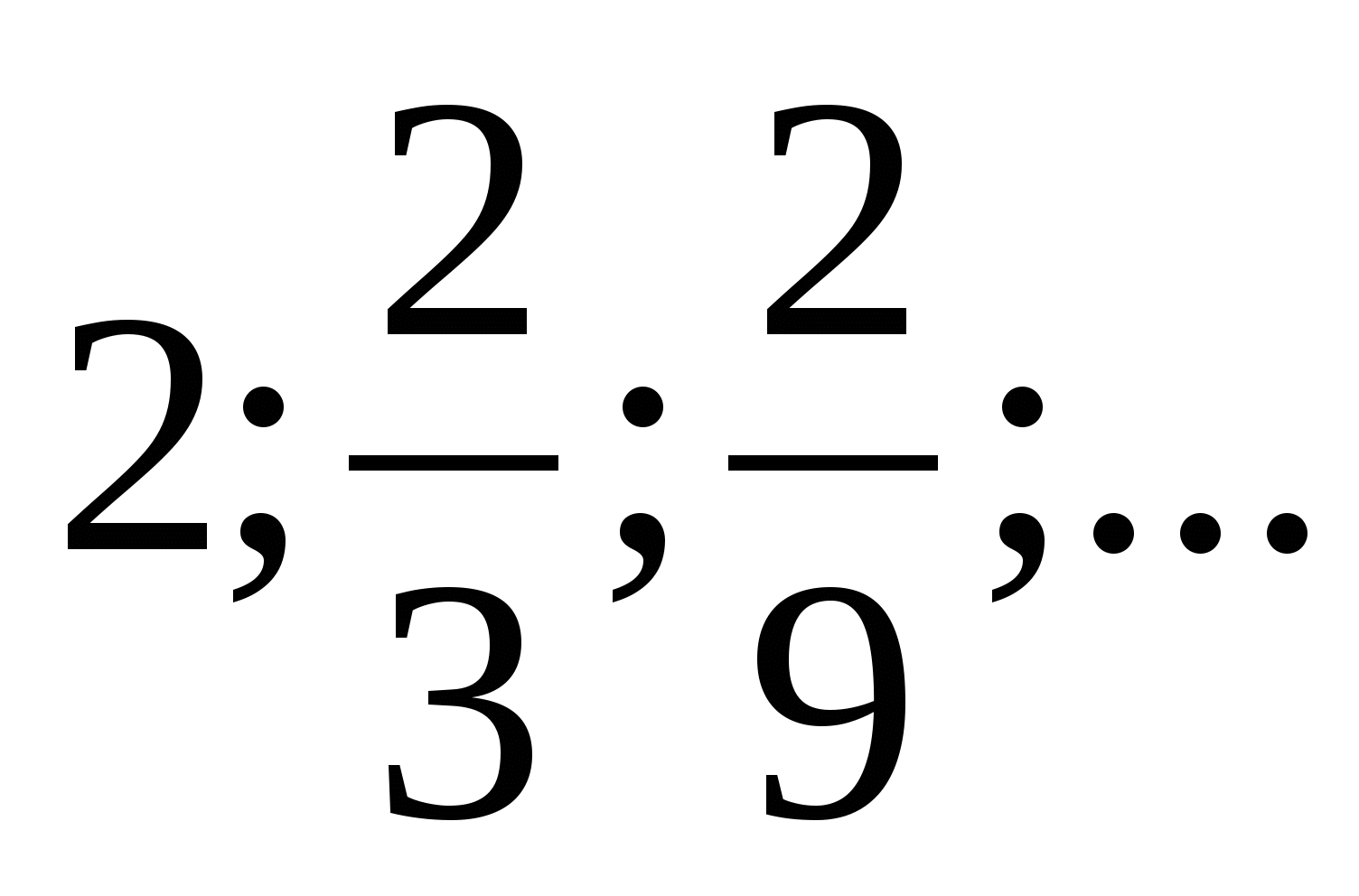найдите пятый член.

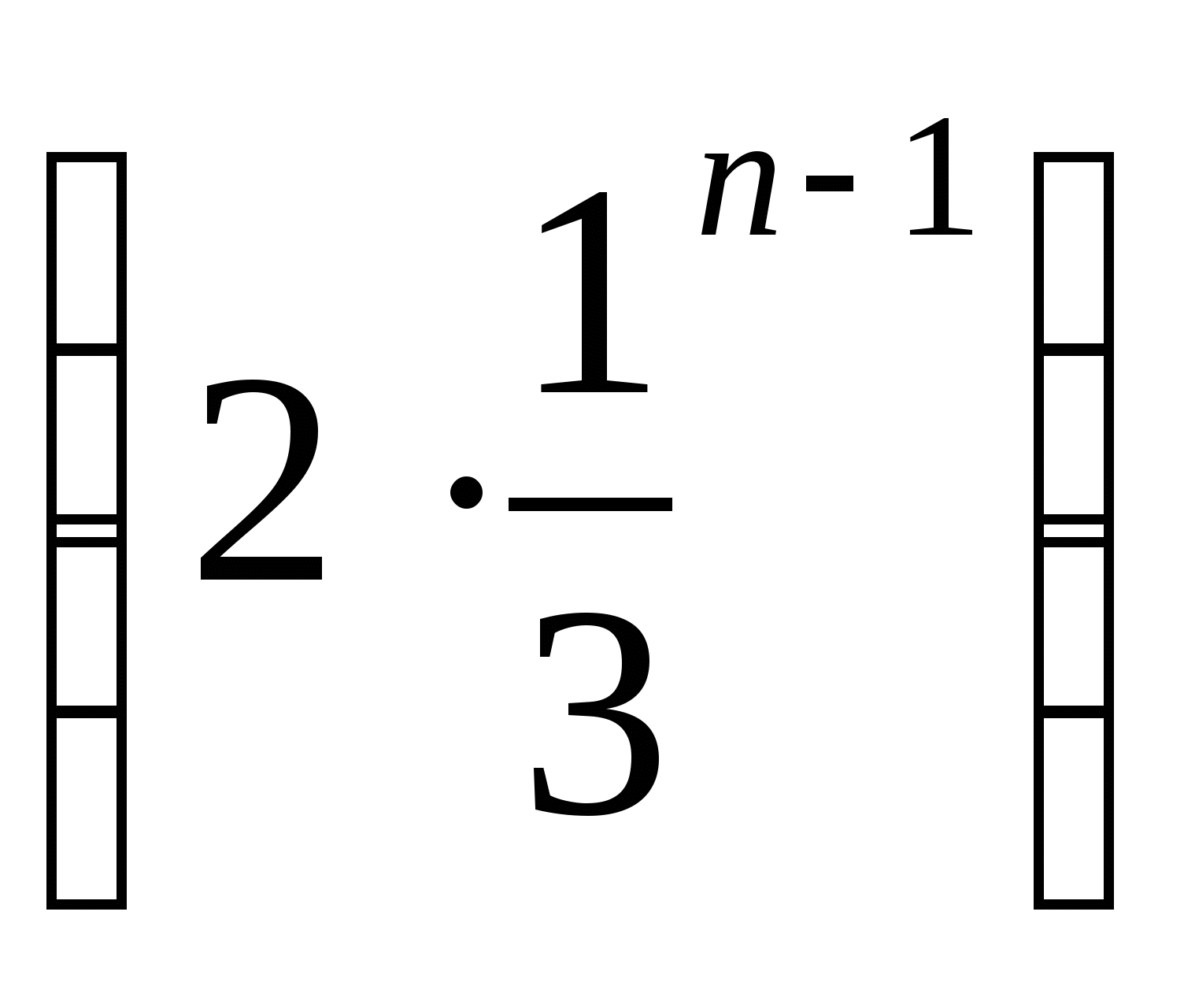2. Для геометрической прогрессии 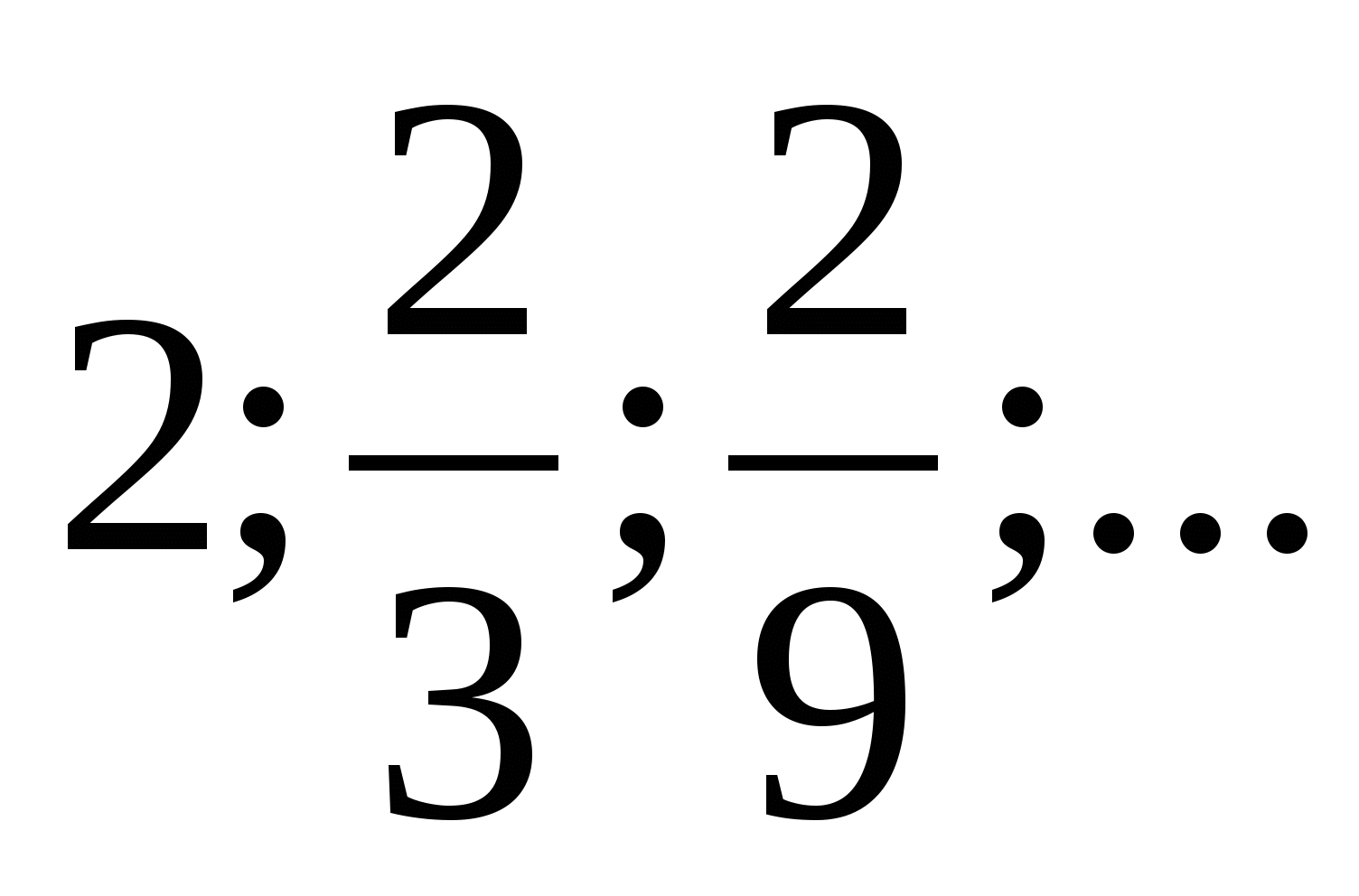найдите n-й член.

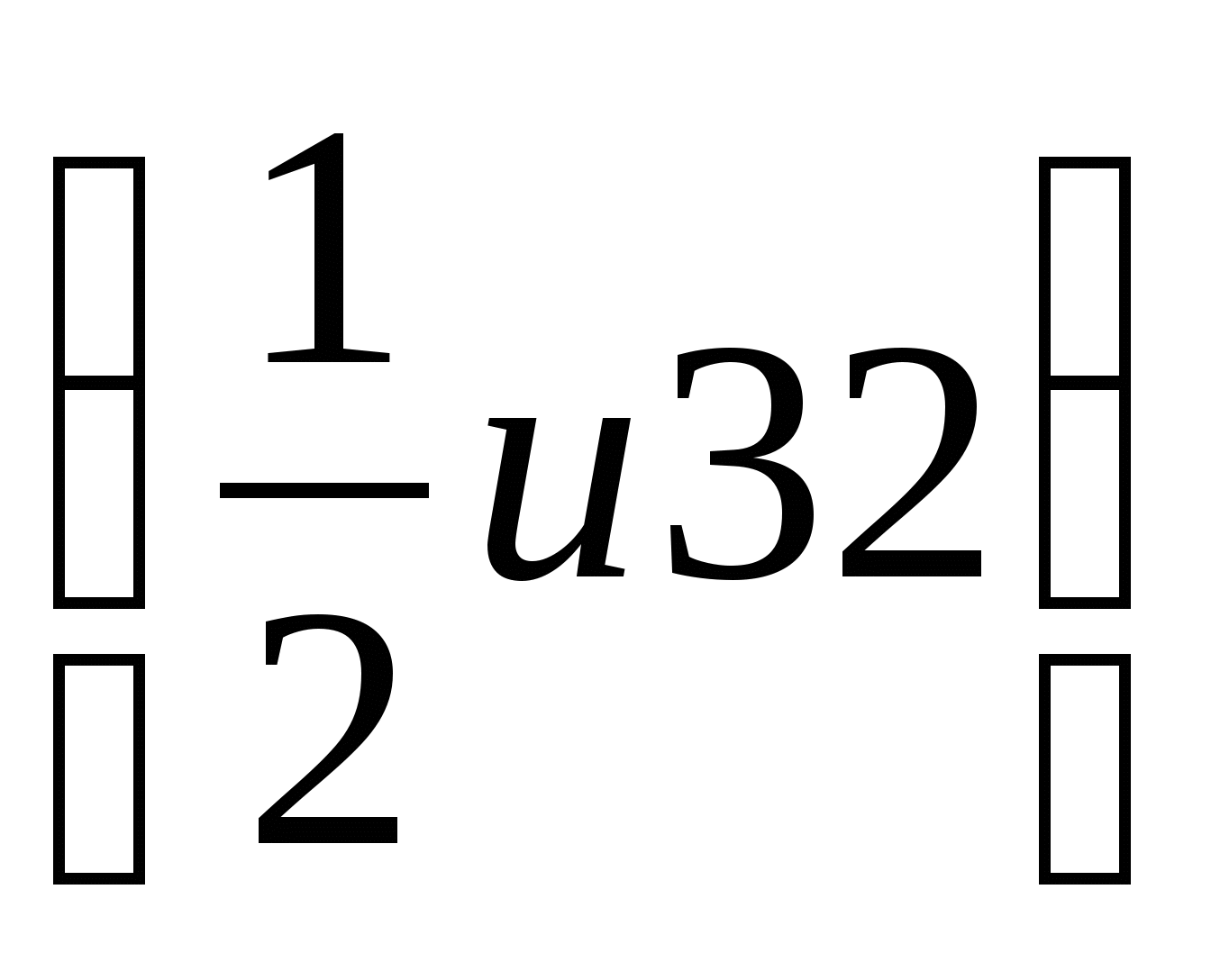3. В геометрической прогрессии b₃= 8 и b₅ = 2. Найдите b₄ (4)

4. В геометрической прогрессии b₃ = 8 и b₅ = 2. Найдите b₁ и q.

5. В геометрической прогрессии b₃ = 8 и b₅ = 2. Найдите S₅. (62)

3. Объяснение нового материала

Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового 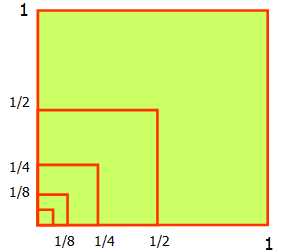квадрата равна половине предыдущего.

В результате, мы получили последовательность сторон квадратов 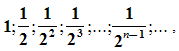образующих геометрическую прогрессию со знаменателем .

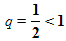И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,

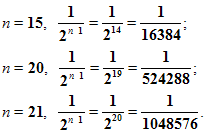
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.

С помощью этого рисунка можно рассмотреть и ещё одну последовательность.

Например, последовательность площадей квадратов:

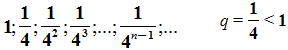
И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.

Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.

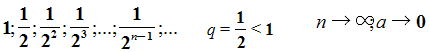
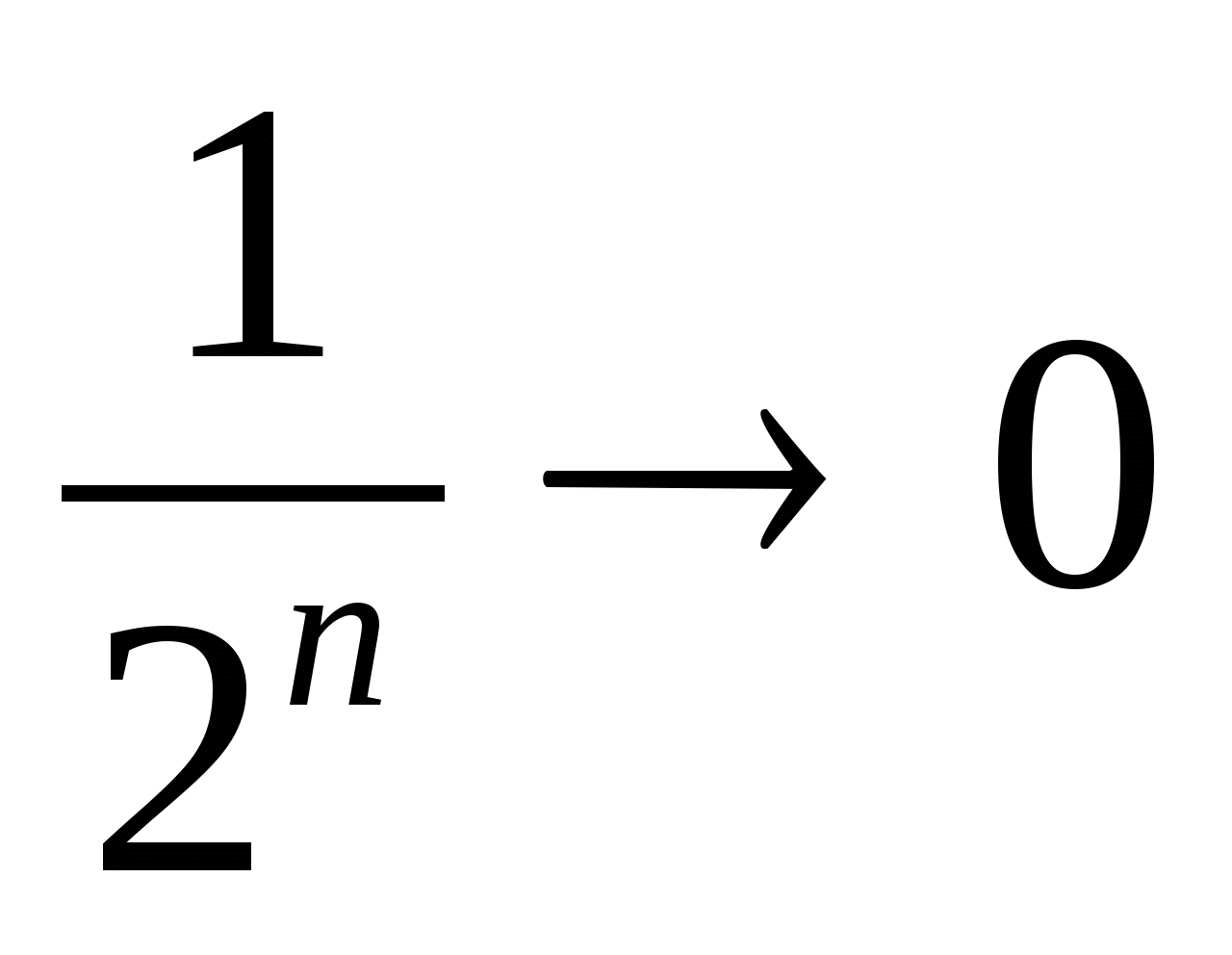при

Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.

То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.

Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.

Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.

Определение:

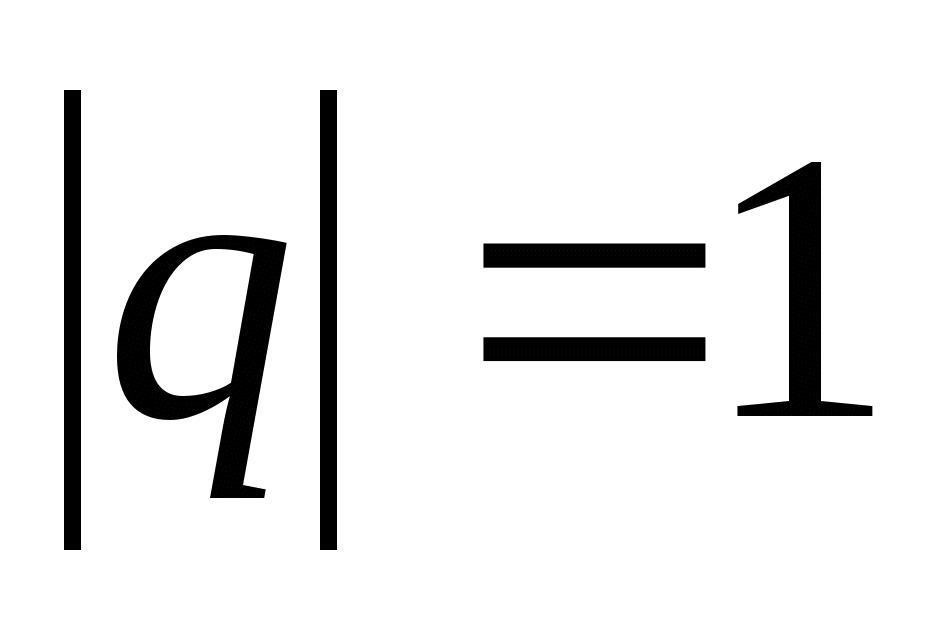Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы. .

С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.

12 3 Следующая ⇒