Контакты

Случайная статья

f (g (x)))' = f' (g (x)) g' (x)

⇐ ПредыдущаяСтр 2 из 2

(f (g (x)))' = f' (g (x)) g' (x)

Содержание и ход работы:

1. Выполнить дифференцирование сложных функций, согласно варианта.

2. Подставить конкретную заданную точку х₀в полученную производную функции; произвести вычисления.

3. Ответить на вопросы по самопроверке.

4. Оформить отчет по выполненной практической работе.

Вариант № 1

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = sin³φ + sin φ ;

fʹ ( ) -?

б) f(х) = cos² x - ln cos x ;

fʹ ( ) -?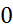

в) f(х) = tg³ x - tg x + x ;

fʹ ( ) -?

г) f(х) = ;

fʹ (2) -?

2. Найдите вторую производную функции в точке:

f(х) = 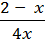; fʹʹ ( ) -?

Вариант № 2

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = ;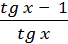

fʹ ( ) -?

б) f(х) = ;

fʹ (-1 ) -?

в) f(х) = (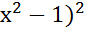

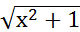
fʹ (1 ) -?

в) f(х) = sin⁴t - cos⁴t;

fʹ ( ) -? ;

2. Найдите вторую производную функции в точке:

f(х) = ; fʹʹ ( ) -?

Вариант № 3

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = ;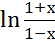

fʹ (3 ) -?

б) f(х) = 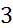сtg x + сtg³ x;

fʹ ( ) -?

в) f(х) = ;

fʹ ( ) -?

г) f(х) = ln tg φ - ;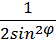

fʹ (2) -?

2. Найдите вторую производную функции в точке:

f(х) = 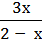; fʹʹ (3) -?

Вариант № 4

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = х ;

fʹ ( ) -?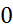

б) f(х) = lg tg x - 2 sin² x;

fʹ ( ) -?

в) f(х) =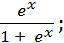

fʹ ( ) -?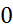

г) f(х) = ln ;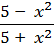

fʹ (2) -?

2. Найдите вторую производную функции в точке:

f(х) = ; fʹʹ ( ) -?

Вариант № 5

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = хln x - x

fʹ ( ) -?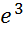

б) f(х) = x· ;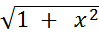

fʹ ( ) -?

в) f(х) = ;

fʹ ( ) -?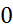

г) f(х) = tg²x - ctg²x

fʹ ( ) -? ;

2. Найдите вторую производную функции в точке:

f(х) = 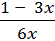; fʹʹ ( ) -?

Вариант № 6

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = ;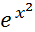

fʹʹ (0) -?

б) f(х) = ln ;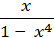

fʹ (2) -?

в) f(х) = 3ctg x + ctg³ x ;

fʹ ( ) -?

г) f(х) = ;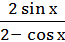

fʹ ( ) -?

2. Найдите вторую производную функции в точке:

f(х) = sin²φ ; fʹʹ ( ) -?

Вариант № 7

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = sin³φ + sin φ ;

fʹ ( ) -?

б) f(х) = sin² x - ln sin x ;

fʹ ( ) -?

в) f(х) = ctg³ x - ctg x ;

fʹ ( ) -?

г) f(х) = ;

fʹ (1) -?

2. Найдите вторую производную функции в точке:

f(х) = cos²φ ; fʹʹ ( ) -?

Вариант № 8

1.Найдите производные сложных функций и вычислите их значения в заданных точках:

а) f(х) = ;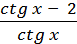

fʹ ( ) -?

б) f(х) = ;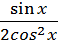

fʹ ( ) -?

в) f(х) = tg⁵x - tg x + x

fʹ ( ) -?

в) f(х) = ;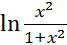

fʹ ( ) -? ;

2. Найдите вторую производную функции в точке:

f(х) = 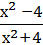; fʹʹ ( ) -?

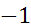Вопросы для самопроверки:

1. а) Для функции у = 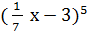найдите у'(0)

б) Для функции у = 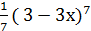найдите у'(0)

2. Каков физический смысл первой производной, второй?

3. В чем состоит геометрический смысл первой производной? Записать уравнение касательной к графику функции в точке х₀.

ЛИТЕРАТУРА.

1. В.В. Пак, Ю.Л. Носенко “Высшая математика” Д.: Сталкер, 1997, с. 181-193.

2.В. А. Кудрявцев, В. П. Демидович «Краткий курс высшей математики!» Наука, 1975, гл. XIII.

3. Ю. М. Почтман Основы математики: учебно-методическое пособие”, М.: МАУП, 1999, с. 57-52.

4. «Курс математики для техникумов ч. 2», ред. Н. М. Матвеева, М.: Наука, 1976, с. 9-14.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.