
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
базовый уровень, время – 3 мин)
2 (базовый уровень, время – 3 мин)
Тема: Построение и анализ таблиц истинности логических выражений.
Про обозначения
К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,), что еще раз подчеркивает проблему.
Что нужно знать:
· условные обозначения логических операций
A, 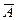 не A (отрицание, инверсия)
не A (отрицание, инверсия)
A Ù B, 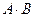 A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)
A Ú B, 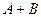 A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)
A→B импликация (следование)
AºB эквивалентность (равносильность)
· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A→B = A Ú Bили в других обозначениях A→B = 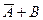
· иногда для упрощения выражений полезны формулы де Моргана:
(A Ù B) = A Ú B 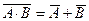
(A Ú B) = A Ù B 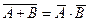
· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»
· таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных
· если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);
· количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно 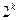 , где
, где 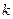 – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
· логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)
· логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)
· логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно
· эквивалентность АºB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1
Пример задания:
Р-21. Логическая функция F задаётся выражением
((x Ù y) Ú (w ® z)) º (z º x).
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение (построение таблицы истинности для F = 1):
1) перепишем выражение, раскрыв импликацию по формуле 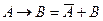 :
: 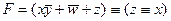
2) сначала предположим, что 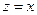 ; в этом случае получаем
; в этом случае получаем
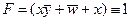
3) так как 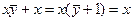 , получим
, получим 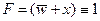 ; при этом значение y может быть любым (1 или 0)
; при этом значение y может быть любым (1 или 0)
4) теперь пусть 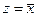 , тогда получаем
, тогда получаем 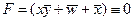
5) используем распределительный закон: 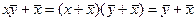 , так что
, так что
 , откуда сразу следует
, откуда сразу следует 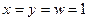 и
и 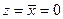 – единственный вариант!
– единственный вариант!
6) этот единственный вариант, для которого 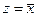 , ОБЯЗАТЕЛЬНО должен быть в приведённой таблице, потому что иначе мы не сможем различить столбцы z и x; это может быть только последняя строчка, куда нужно добавить две единицы:
, ОБЯЗАТЕЛЬНО должен быть в приведённой таблице, потому что иначе мы не сможем различить столбцы z и x; это может быть только последняя строчка, куда нужно добавить две единицы:
| z | ? | ? | ? | F |
7) в остальных строчках должно вполняться равенство 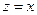 , значит x – точно не второй столбец (не подходит вторая строка)
, значит x – точно не второй столбец (не подходит вторая строка)
8) предположим, что x – третий столбец, и в свободной ячейке – нуль:
| z | ? | x | ? | F |
9) при этом для остальных двух столбцов в этих строчках должно выполняться условие 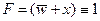 , а оно не может выполняться – при любом варианте в одной строке сумма
, а оно не может выполняться – при любом варианте в одной строке сумма 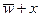 равна 0; значит x – последний столбец, и в первой строке z = 1:
равна 0; значит x – последний столбец, и в первой строке z = 1:
| z | ? | ? | x | F |
10) чтобы разобраться с поcледними двумя столбцами снова вспомним, что при 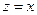 должно выполняться условие
должно выполняться условие 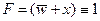 ; это возможно только тогда, когда второй столбец – это y, а третий - w
; это возможно только тогда, когда второй столбец – это y, а третий - w
11) Ответ: zywx
Решение (А.Н. Носкин, заполнение исходной ТИ и анализ полной таблицы истинности для F = 1):
1) в выражении 4 логических переменных, тогда всех решений будет 16 (24).
| x | y | w | z |
2) подставим набор значений логических переменных и удалим все решения, которые не дают в ответе F = 1
| x | y | w | z |
Получаем 7 решений. Анализируя ТИ исходной функции видим, что набора 0 0 0 0 и 1 1 1 1 нет. Уберем их из ТИ решений.
| x | y | w | z |
3) В ТИ решений только одна строка имеет три нуля, тогда сравнивая с ТИ исходной функции видим, что 1 соответствует Y.
| ? | Y | ? | ? | F |
4) ДОЗАПОЛНИМ таблицу истинности исходной функции (желтая заливка) на основе анализа ТИ решений, а именно т.к больше строк с тремя «0» нет, то в первой строке в пустой ячейке будет «1». И раз нет больше строк с двумя «0», то в третьей строке пустые ячейки равны «1».
| ? | Y | ? | ? | F |
5) Анализируя 1ю строку выше приведенной таблице и ТИ решений видим, что строка с двумя «0» всего одна, из которых один нуль известен - это Y, тогда второй это – W;
| ? | Y | W | ? | F |
6) Далее рассуждая видим, что в ТИ решений (кроме столбца Y) один «0» имеет – Х, тогда последний столбец – это Х, а первый столбец – Z.
7) Ответ: zywx
Ещё пример задания:
Р-20. Логическая функция F задаётся выражением
((x Ù y) Ú (y Ù z)) º ((x ® w) Ù (w ® z)).
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение (построение таблицы истинности для F = 1):
1) запишем выражение в более понятной форме: 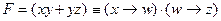
2) попробуем найти все сочетания переменных, при которых функция равна 1 (их должно быть не очень много)
3) при x = 0 получаем 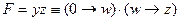 ; импликация с нулём в левой части всегда истинна (из лжи следует всё, что угодно), поэтому
; импликация с нулём в левой части всегда истинна (из лжи следует всё, что угодно), поэтому 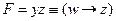
4) пусть теперь ещё z = 0, тогда 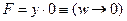 , что истинно при w = 1 и при любом y;
, что истинно при w = 1 и при любом y;
5) пусть теперь x = 0 и z = 1, тогда 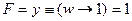 , что истинно при y = 1 и при любом w;
, что истинно при y = 1 и при любом w;
6) из 4 и 5 получаем такие строки в таблице истинности исходной функции:
| x | y | z | w | F |
7) остаётся рассмотреть случай, когда x = 1, при этом 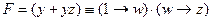
8) учитываем, что 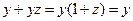 и
и  ; получаем
; получаем 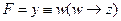
9) преобразуем импликацию 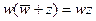 , так что
, так что 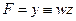
10) для y = 0 это выражение истинно при (w, z) = (0,0), (0,1) и (1,0), а для y = 1 – только при w = z = 1, это даёт ещё 4 строки в таблице истинности
| x | y | z | w | F |
11) итак, у нас есть 8 строк в таблице истинности, где функция равна 1:
| x | y | z | w | F |
попробуем сопоставить их с заданными в условии строками:
| ? | ? | ? | ? | F |
12) замечаем, что есть одна характерная строка с тремя единицами; кроме того, поскольку все строки различны, в одной из пустых ячеек должен стоять 0, а во второй – 1
13) в полученной нами таблице видим единственную строку с тремя единицами, что сразу позволяет определить, что первый столбец – это x, который всегда равен 0:
| x | y | z | w | F |
14) теперь из оставшихся двух строк остаётся найти 2 строки, значения которых различаются только в одном столбце; под это условие подходит только пара двух верхних строк, они различаются в столбце y – из исходной таблицы видим, что это 4-й столбец
15) также из исходной таблицы видим, что во втором столбце в этих двух строках единицы – это w, тогда третий столбец – это z
16) Ответ: xwzy.
Решение (А.Н. Носкин, построение таблицы истинности для F = 1):
1) запишем выражение в более понятной форме: 
2) вынесем y за скобки: F = (y*(x+z) ≡ ((x→w)*(w→z))
3) F = 1, при 0=0 и 1=1. Тогда составим ТИ для левой части выражения равные 0 и 1.
| y | x | z |
| y | x | z |
4) Объединим эти таблицы, подключим переменную w и уберем из таблицы строки, при которых F=0 после подключения переменной w.
| y | x | z | w |
5) Получилось 8 всевозможных решений.
6) Обратим внимание, что по условию у нас нет повторяющихся строк, но в таблице есть строки с тремя одинаковыми ячейками, тогда можно ДОЗАПОЛНИТЬ таблицу истинности исходной функции (желтая заливка) в одну из них вставив 0, в другую 1.
| ? | ? | ? | ? | F |
7) Анализ строк таблицы истинности исходной функции показывает:
- строки, состоящей из четырех «1» нет, поэтому ее можно убрать (красная заливка);
- только одна строка имеет в ячейках три единицы и один «0». И в ТИ всех решений (желтая заливка) этот «0» будет соответствовать Х в ТИ исходной функции.
| y | x | z | w |
8) Так как мы определили, что первый столбец соответствует Х и содержит только «0», то строки ТИ решений с «1» в столбце Х – удалим (синяя заливка)
| y | x | z | w |
и получим ТИ меньшего размера.
| y | x | z | w |
9) Анализ столбцов ТИ исходной функции показывает, что одна «1» в третьем столбце соответствует Z, а в третьей строке ТИ исходной функции две неизвестные переменные противоположны «0» и «1», что соответствует W и Y, так как X и Z уже определены и равны «0» (зеленая заливка)
| y | x | z | w |
10) Ответ: xwzy.
Ещё пример задания:
Р-19. Логическая функция F задаётся выражением
((w Ú y) º x) Ú ((w ® z) Ù (y ® w)).
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
1) запишем выражение в более понятной форме: 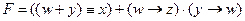
2) попробуем найти все сочетания переменных, при которых функция равна 0 (их должно быть не очень много)
3) выберем для начальной подстановки переменную, которая чаще всего встречается в выражении и поэтому подстановка её значения даст наибольшую информацию; у нас это переменная w
4) подставим сначала w = 0, а затем w = 1, и таким образом построим все строки таблицы истинности, где функция равна нулю
5) при w = 0 получаем 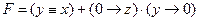
поскольку 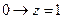 при всех z, имеем
при всех z, имеем 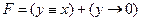
6) для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
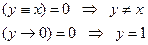
7) таким образом, при w = 0 получаем y = 1, x = 0, а значение z может быть любое; это даёт две строки в таблице истинности:
| x | y | z | w | F |
8) теперь рассмотрим случай, когда w = 1: получаем 
поскольку 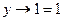 при всех y, имеем
при всех y, имеем 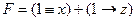
9) для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
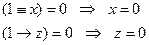
10) таким образом, при w = 1 получаем x = 0, z = 0, а значение y может быть любое; добавляем ещё две строки в таблицу истинности:
| x | y | z | w | F |
11) сравниваем эту таблицу с таблицей в задании:
| F | ||||
12) две единицы могут быть только в столбцах y и w, поэтому это столбцы 1 и 4
13) кроме этих столбцов единственная единица может быть в столбце z, поэтому столбец 3 – это z
14) при z = 1 должно быть y = 1, поэтому столбец 1 – это y, а столбец 4 – это w
15) остаётся столбец 2 – это x
16) Ответ: yxzw.
Решение (разбиение на два слагаемых, А.Н. Носкин):
1) запишем выражение в более понятной форме: 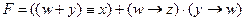
2) Каждое из слагаемых скобок должна быть равна 0, поэтому составим для каждой таблицу истинности.
3) Рассмотрим ((w ® z) Ù (y ® w)), а именно первую скобку (w ® z), она равна 0 при ситуации 1 ® 0, тогда y во второй скобке может быть любым
| w | z | y |
Теперь рассмотрим вторую скобку (y ® w), она равна 0 при ситуации 1 ® 0, тогда z во первой скобке может быть любым. Добавим эти значения в таблицу истинности, которая приведена выше.
| w | z | y |
4) Теперь рассмотрим ((w Ú y) º x). Эта скобка будет равна 0 при ((w Ú y) ≠ x). Составим таблицу истинности
| w | y | x |
Анализ этой таблицы показывает, что набора 001 (выделено цветом) быть не может иначе система будет равна 1 по скобке ((w ® z) Ù (y ® w)).
5) Сравним полученные таблицы истинности с исходной таблицей в задании:
| F | ||||
6) x в таблице истинности во всех строках равен 0, тогда он соответствует второму столбцу, так как там нет ни одной единицы. Сразу заполним нулями.
| x | F | |||
7) w и y в таблице истинности имеют 2 и более единицы, а z всего 1, тогда z - это столбец 3. Заполним сразу 0.
| x | z | F | ||
8) Так как строки не повторяются, то в первой ячейке второй строки может быть только 0. Заполним ее.
| x | z | F | ||
9) Теперь проанализируем последнюю ячейку третьей строки. Ее значения могут быть 0 и 1. Предположим, что там 0, а в первом столбце w, тогда выражение примет вид
((1 Ú 0) º 0) Ú ((1 ® 1) Ù (0 ® 1)) – этого быть не может, так как выражение равно 1. Предположим, что там 1 и в первом столбце w, тогда выражение примет вид
((1 Ú 1) º 0) Ú ((1 ® 1) Ù (1 ® 1)) – этого быть не может, так как выражение равно 1. Таким образом в первом столбце w не может быть ни при каком случае. Там только y, ну а w отправляется в 4-й столбец.
10) Ответ: yxzw.
Ещё пример задания:
Р-18. Логическая функция F задаётся выражением (x Ú y) ® (y º z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| ? | ? | ? | F |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
1) запишем выражение в более понятной форме: 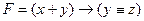
2) для решения этой задачи используем свойство операции «импликация»: 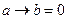 тогда и только тогда, когда a = 1 и b = 0
тогда и только тогда, когда a = 1 и b = 0
3) в обеих строках приведённой части таблицы функция равна 0, поэтому везде
· хотя бы одна из величин, x или y равна 1, что даёт 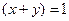 ;
;
· y и z различны, что даёт 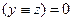
4) поскольку значения в первых двух столбцах в первой строке равны 0, один из этих столбцов – это x
5) предположим, что x – это первый столбец:
| x | ? | ? | F | |
тогда в обеих строках получаем 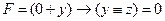 , откуда сразу следует, что есть единственная пара остальных переменных, удовлетворяющих условию задачи: y = 1, z = 0, и вторая строка олжна быть копией первой (второй подходящей пары y , z нет!), что противоречит условию
, откуда сразу следует, что есть единственная пара остальных переменных, удовлетворяющих условию задачи: y = 1, z = 0, и вторая строка олжна быть копией первой (второй подходящей пары y , z нет!), что противоречит условию
6) это значит, что x – это не первый, а второй столбец:
| ? | x | ? | F | |
7) если при этом предположить, что первый столбец – это y, то в первой строке получаем  (при любом z!), что противоречит условию; поэтому первый столбец – это z, а третий – y
(при любом z!), что противоречит условию; поэтому первый столбец – это z, а третий – y
8) на всякий случай проверяем первую строку: 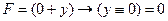 справедливо при y = 1
справедливо при y = 1
9) во второй строке условие 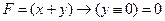 справедливо при x = 1 и y = 1 (что отличается от варианта в первой строке значением x)
справедливо при x = 1 и y = 1 (что отличается от варианта в первой строке значением x)
10) Ответ: zxy.
Решение (построение части таблицы истинности, С.В. Логинова):
1) По свойству импликации функция имеет значение 0 тогда, когда в первой скобке получится 0, а во второй 1. Из этого следует что возможные сочетания для переменных x и y равны 01, 10, 11.
2) Вторая скобка равна 0, если y и z имеют разные значения.
3) Составим таблицу истинности для всех возможных вариантов.
| x | y | z | F |
4) Из получившейся таблицы истинности мы видим, что только одна строка этой таблицы содержит 2 нуля и одну 1 в исходных данных. Эта единица – переменная y, значит третий столбец y. Среди столбцов только один содержит два нуля – столбец z. Отсюда следует, что первый столбец – z.
5) Ответ: zxy
Решение (метод исключения, С.Н. Лукин, г. Москва):
1) всего возможно 6 вариантов решения задачи:
| x | y | z |
| x | z | y |
| y | x | z |
| y | z | x |
| z | x | y |
| z | y | x |
В процессе решения будем вычеркивать лишние варианты, пока не останется один-единственный. Также будем по возможности заполнять пустые клетки таблицы (по принципу «Чем меньше неопределенностей, тем лучше»).
2) используем следующее свойство импликации: выражение a®b равно нулю тогда и только тогда, когда a=1 и b=0. В нашем примере a это левая скобка, b – правая.
3) теперь рассуждаем от противного. Пусть в пустой клетке первой строки таблицы истинности стоит ноль:
| ? | ? | ? | F |
4) Тогда в любом из 6 вариантов решения получится x = 0 и y = 0, а значит (x Ú y)=0, что противоречит упомянутому свойству импликации. Значит, там стоит единица:
| ? | ? | ? | F |
5) По той же причине в левых двух столбцах первой строки не могут находиться одновременно x и y. Это позволяет нам вычеркнуть два из шести вариантов решения:
    | | |
| | | |
Остаются 4 варианта:
| x | z | y |
| y | z | x |
| z | x | y |
| z | y | x |
6) Идем дальше. По упомянутому свойству импликации вторая скобка должна равняться 0, а значит y и z не должны совпадать. Это позволяет нам, погдядев на первую строку таблицы истинности, вычеркнуть еще два варианта решения:
| | | |
| | | |
Остаются 2 варианта:
| x | z | y |
| z | x | y |
7) Получается, что в правом столбце обязательно стоит y. Начало положено.
8) Попробуем заполнить пустые клетки во второй строке таблицы истинности. Способов заполнения четыре: 00, 01, 10, 11. Первый из них мы рассмотрели выше, он отпадает. Второй отпадает, так как в этом случае две строки таблицы истинности будут совпадать, что противоречит условию задачи. Третий и четвертый способы приказывают нам иметь во втором столбце единицу. Спасибо и на этом:
| ? | ? | y | F |
9) Теперь рассмотрим первый из двух оставшихся вариантов решения (xzy), подставив сначала в пустую клетку ноль. Но ноль отпадает, так как x и y не могут одновременно равняться нулю. А единица отпадает, так как y и z не должны совпадать. Значит, отпадает и сам вариант решения xzy. Следовательно, решением задачи является единственный невычеркнутый вариант: zxy.
10) Из тех же соображений, что y и z не должны совпадать, в оставшуюся пустую клетку ставим единицу:
| z | x | y | F |
11) А теперь проверьте решение, подставив в выражение (x Ú y) ® (y º z) значения переменных из каждой строки таблицы.
12) Ответ: zxy.
Решение (метод инверсии, А.Н. Носкин, г. Москва):
1) Известно, что если F = 0, то обратная её функция 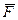 =1.
=1.
2) Применим закон де Моргана и упростим:
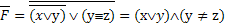
3) тогда при тех же значениях аргументов функция 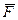 истинна
истинна
| ? | ? | ? | 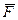
|
4) анализ формулы  показывает, что для истинности функции
показывает, что для истинности функции 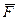 необходимо, чтобы значение в каждой скобке были равны 1.
необходимо, чтобы значение в каждой скобке были равны 1.
5) Кроме того, этот анализ показывает, что в первой строке таблицы, в ее последнем столбце, не может быть 0, так как тогда значение функции не будет равно 1. На основе этого анализа таблица примет вид:
| ? | ? | ? | 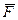
|
6) Анализ первой строки данной таблицы показывает, что в первых двух ячейках не может быть одновременно ни x, ни y. В этих ячейках рядом может быть только x и z, значит y находится в последней ячейке.
7) Во второй ячейке, второй строки не может быть 0, так как должны быть неповторяющиеся строки,а все нули быть не могут (не выполнится условие 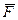 =1). Значит в данной ячейке строго 1.
=1). Значит в данной ячейке строго 1.
| ? | ? | y | 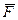
|
8) Значит в оставшейся ячейке может быть только 0 или 1, а именно, во второй строке возможен набор 010 или 011. Простой анализ с учетом того, что в последнем столбце y, дает итоговый ответ – набор 011 .
9) Ответ: zxy.
Ещё пример задания:
Р-17. Логическая функция F задаётся выражением x Ú y Ú (z Ù w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
1) запишем выражение в более понятной форме: 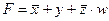
2) анализ формулы 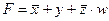 показывает, что для того, чтобы функция F была ложна, необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
показывает, что для того, чтобы функция F была ложна, необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
| y | ? | ? | x | F |
3) остается разобраться с двумя средними столбцами; обратим внимание на вторую строчку таблицы, в которой одна из оставшихся переменных равна 1, а вторая – 0; так как функция равна 0, то  , откуда следует, что z = 1 и w = 0 (иначе произведение будет равно 1)
, откуда следует, что z = 1 и w = 0 (иначе произведение будет равно 1)
4) Ответ: yzwx.
Решение (2 способ, инверсия выражения):
1) запишем выражение в более понятной форме: 
2) попытаемся свести задачу к уже известной задаче; если при каком-то наборе аргументов функция F ложна, то обратная её функция, 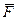 , истинна
, истинна
3) построим обратную функцию, используя законы де Моргана:
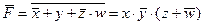
4) тогда при тех же значениях аргументов функция 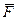 истинна
истинна
| ? | ? | ? | ? | 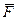
|
5) анализ формулы 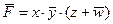 показывает, что для истинности функции
показывает, что для истинности функции 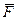 необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
| y | ? | ? | x | 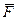
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|