Практическое занятие. неделя). ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ. Термины и определения. Сущность метода проекций с числовыми отметками. Заложение и интервал прямой

Стр 1 из 2Следующая ⇒

Практическое занятие

(9-10 неделя)

А. теоретический материал

Объяснить на практическом занятии

1. ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ

1.1. Термины и определения

Сущность метода проекций с числовыми отметками

Сущность метода заключается в ортогональном проецировании геометрического объекта на одну, чаще горизонтальную, плоскость проекций, называемую плоскостью нулевого уровня П0 с указанием численного значения расстояния (обычно в метрах) от характерных точек объекта до данной плоскости проекций в единицах указанного линейного масштаба (рис. 1, а).

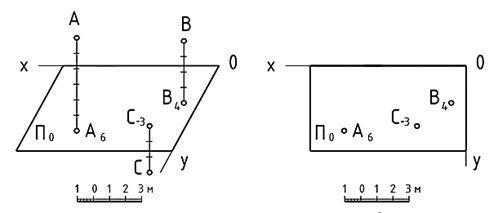
Рис.

Заложение и интервал прямой

Длину горизонтальной проекции прямой называют заложением и обозначают буквой L (рис. 3 ), а ∆ h – превышением точки А над точкой В, ∆ h = hA – hВ. Уклон прямой i равен тангенсу угла α, являющемуся углом наклона прямой к плоскости П0 (или углом падения прямой):

i = tgα = ∆ h / L.

Уклон может быть задан дробью, в градусах, процентах, а также в промилле (10/00 = 0,001).

Заложение прямой, приходящееся на единицу превышения, называют интервалом прямой и обозначают буквой l. Интервал необходимо знать, чтобы на заложении прямой можно было определить отметки с целочисленными значениями. Для этого проекцию прямой нужно проградуировать. Градуирование прямой – это действия по установлению интервала прямой.

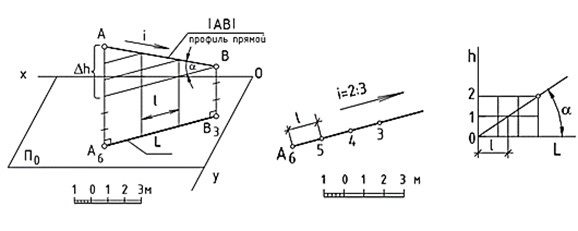
Рис.

12 Следующая ⇒