
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
октября 2020 г. (четверг) . Задание 1. Подготовить таблицу к решению задачи оптимального планирования.
22 октября 2020 г. (четверг)
Дисциплина: Информатика и ИКТ
Группа: № 74
Урок № 20
Тема: Практическая работа № 4: « Решение задачи оптимального планирования в MS Excel».
Цель: получить представление о построении оптимального плана методом линейного программирования, практически освоить средство Microsoft Excel Поиск решения для построения оптимального плана.
Учебник: Информатика. Базовый уровень : ученик для 11 класса / И.Г. Семакин, Е.К. Хеннер, Т.Ю. Шеина. – 5-е изд. – М. : БИНОМ. Лаборатория знаний, 2015. – 224 с. : ил.
Используемое программное обеспечение: табличный процессор Microsoft Excel.
 Справочная информация
Справочная информация
Средство, которое используется в данной работе, называется Поиск решения. Соответствующая команда находится в меню Сервис —> Поиск решения — одно из самых мощных средств табличного процессора Excel. Покажем на простейшем примере («пирожки и пирожные», см. § 20), как воспользоваться указанным средством.
Задание 1
Реализовать поиск оптимального решения для задачи планирования работы школьного кондитерского цеха, описанной в § 20 учебника.
1. Подготовить таблицу к решению задачи оптимального планирования.
В режиме отображения формул таблица показана на рисунке. Ячейки В5 и С5 зарезервированы соответственно для значений x (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже представлена система неравенств, определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция занесена в ячейку В15.
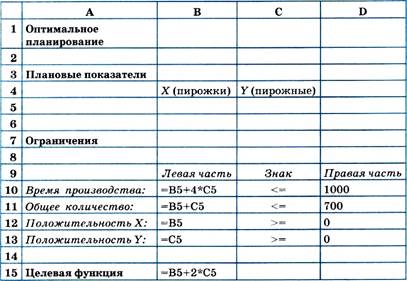
2. Вызвать программу оптимизации и сообщить ей, где расположены данные. Для этого выполнить команду Сервис —> Поиск решения. На экране откроется соответствующая форма:

3. Выполнить следующий алгоритм:
=> ввести адрес ячейки с целевой функцией. В нашем случае это В15 (заметим, что если перед этим установить указатель мыши на ячейку В15, то ввод произойдет автоматически);
=> поставить отметку максимальному значению, т. е. сообщить программе, что нас интересует нахождение максимума целевой функции;
=> в поле Изменяя ячейки ввести В5 : С5, т. е. сообщить, какое место отведено под значения переменных — плановых показателей;
=> в поле Ограничения ввести неравенства-ограничения, которые имеют вид: B10 <= D10; B11 <= D11; B12 >= D12; B13 >= D13.
Ограничения вводятся следующим образом:
☛ щелкнуть на кнопке Добавить;
☛ в появившемся диалоговом окне Добавление ограничения ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10;
☛ снова щелкнуть на кнопке Добавить и аналогично ввести второе ограничение B11 <= D11 и т. д.;
☛ в конце щелкнуть на кнопке ОК;
=> закрыть диалоговое окно Добавление ограничения. Перед нами снова форма Поиск решения:

=> указать, что задача является линейной (это многократно облегчит программе ее решение). Для этого щелкнуть на кнопке Параметры, после чего откроется форма Параметры поиска решения:

=> установить флажок линейная модель. Остальная информация на форме Параметры поиска решения чисто служебная, автоматически устанавливаемые значения нас устраивают, и вникать в их смысл не будем. Щелкнуть на кнопке ОК. Снова откроется формаПоиск решения;
=> щелкнуть на кнопке Выполнить — в ячейках В5 и С5 появится оптимальное решение:
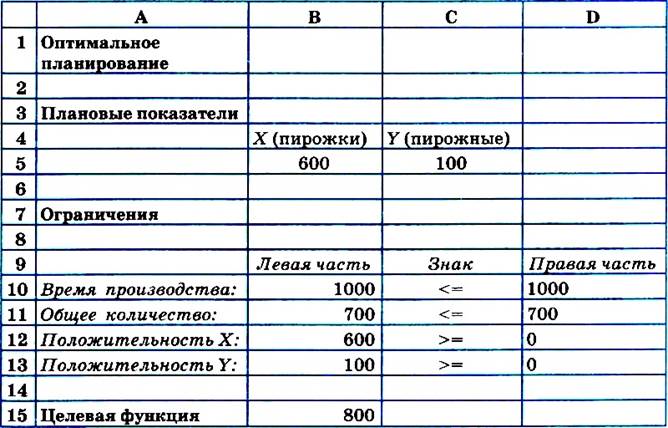
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|