f(x, у) = х + 2у. (2). ВНИМАНИЕ!!!

f(x, у) = х + 2у. (2)

Следовательно, получение оптимального плана свелось к следующей математической задаче:

Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2) .

Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.

Теперь следующий вопрос: как решить эту задачу? Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода.

Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию f(x, у) величины хну входят линейно (т. е. в первой степени), наша задача относится к разделу этой науки, который называется линейным программированием.

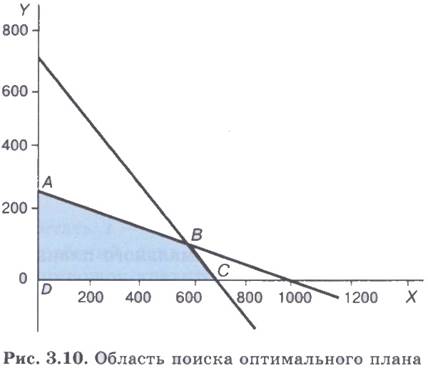
Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:

х + 4у = 1000,

х + у = 700,

х = 0 (ось У).

у = 0 (ось X)

На рис. 3.10 эта область представляет собой четырехугольник ABCD и выделена заливкой. Любая точка четырехугольника является решением системы неравенств (1). Например, х = 200, у = 100. Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке (x = 600, у = 50) соответствует f(600, 50) = 700. Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.

В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума.

В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис. 3.10. В этой точке значение целевой функции f(600, 100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.

Домашнее задание:

1. Ответьте устно на вопросы:

а) В чем состоит задача оптимального планирования?
б) Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

в) С помощью какого средства табличного процессора Microsoft Excel можно решать задачи оптимального планирования?

Конспект сфотографировать и прислать в ВКонтакте:

1. Елене Анатольевнев ЛС.

2. Александру Седнёву в ЛСили на электронную почту sednyov@mail.ru Зайти на электронную почту можно здесь .

ВНИМАНИЕ!!!

При составлении конспекта обязательно!!! вначале написать свою фамилию и имя (можно простым карандашом), дату урока, номер урока, а затем текст.

Образец оформления самостоятельной работы:

Иванова Анна Урок № 25 Дата: 20.03.20 Самотоятельная работа Вакуум – состояние газа, при котором молекулы успевают пролететь от одной стенки сосуда к другой, ни разу не испытав соударение друг с другом. …………………………………………………………………………………………………………… И так далее.

⇐ Предыдущая 123 4 Следующая ⇒