- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Биквадратное уравнение
Биквадратное уравнение
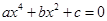решается сведением к квадратному уравнению с помощью введения новой переменной. пусть 
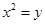, тогда имеем 
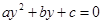и решается квадратное уравнение относительно y.
Например.
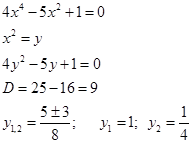
и тогда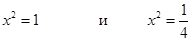 
, решаем эти уравнения:
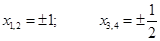получили четыре действительных корня. Ответ: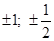 
Решить самостоятельно:
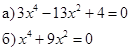
Уравнение третьей степени и имеет 3 корня. Как их найти? Разложим левую часть уравнения на множители.
Применяем формулу: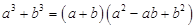 
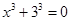
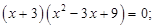произведение равно нулю, если хотя бы один из сомножителей равен нулю, т.е.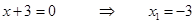 
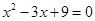
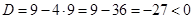действительных корней нет.
т.е. уравнение имеет один действительный корень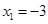 
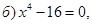разложим на множители 
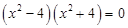имеем:
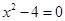или 
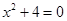
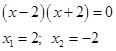
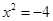действительных корней нет.
Ответ: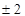 
.
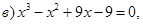группируем члены
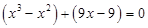выносим общий множитель из каждой скобки
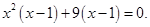
Вынесем 
за скобки
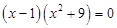и тогда
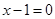или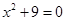 
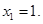
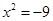
Ответ: 1.
|
|
|
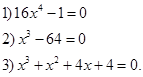
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|