
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнения и их свойства. Линейные уравнения, квадратные уравнения и приводимые к ним. Дробно- рациональные уравнения.
Уравнения и их свойства. Линейные уравнения, квадратные уравнения и приводимые к ним. Дробно- рациональные уравнения.
План.
1. Уравнения и их свойства.
2. Линейные уравнения, квадратные уравнения и приводимые к ним.
3. Дробно- рациональные уравнения.
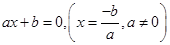 – линейное уравнение I степени с одной переменной
– линейное уравнение I степени с одной переменной
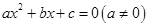 – уравнение II степени с одной переменной
– уравнение II степени с одной переменной
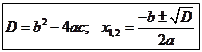
Решить уравнение – значит найти множество его корней или доказать, что их нет. это множество называют решением уравнения.
Два уравнения называются равносильными если решение (корень) одного уравнения является решением (корнем) другого уравнения и наоборот.
Уравнения 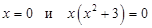 равносильны, так как оба имеют единственный корень
равносильны, так как оба имеют единственный корень 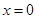 .
.
Уравнения 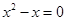 и
и 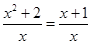 – неравносильны, так как
– неравносильны, так как 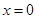 является корнем первого уравнения, но не удовлетворяет второму уравнению.
является корнем первого уравнения, но не удовлетворяет второму уравнению.
Уравнения 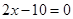 и
и 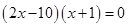 неравносильны, так как корень первого уравнения
неравносильны, так как корень первого уравнения 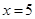 , а второе уравнение кроме этого корня имеет еще корень
, а второе уравнение кроме этого корня имеет еще корень 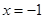 , который не является корнем первого уравнения.
, который не является корнем первого уравнения.
Решим уравнения:
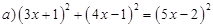
раскроем скобки, применяя формулы сокращенного умножения 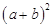 и
и 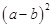
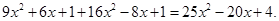
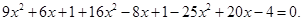
приведем подобные члены, получим
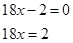
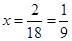 Ответ:
Ответ: 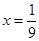 – корень уравнения.
– корень уравнения.
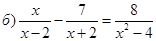 разложим
разложим 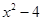 на множители
на множители
перенесем все члены уравнения в левую часть и приведем дроби к общему знаменателю
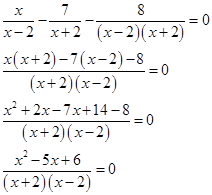
дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, т. е.
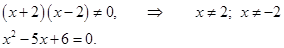
Решаем уравнение
 (корни можно найти по теореме Виета)
(корни можно найти по теореме Виета)
Так как 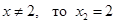 – посторонний корень и решением уравнения будет
– посторонний корень и решением уравнения будет 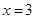 . Ответ:
. Ответ: 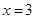 .
.
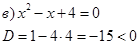
уравнение не имеет действительных корней.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|