
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Б. Открытая модель
Б. Открытая модель
Целевая функция 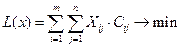 (4.7)
(4.7)
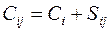 (4.8)
(4.8)
Ограничения 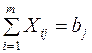 (4.9)
(4.9)
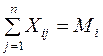 (4.10)
(4.10)
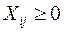 (4.11)
(4.11)
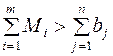 (4.12)
(4.12)
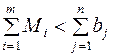 (4.13)
(4.13)
где 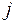 =1,2, …, n - потребители (заводы районы, пункты и т.д.);
=1,2, …, n - потребители (заводы районы, пункты и т.д.); 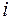 =1,2, ..m – заводы-изготовители; Xij – величина поставки
=1,2, ..m – заводы-изготовители; Xij – величина поставки 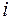 -го завода-изготовителя
-го завода-изготовителя 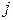 -му потребителю;
-му потребителю; 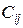 – совокупные затраты на производство и доставку единицы продукции с
– совокупные затраты на производство и доставку единицы продукции с 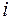 -го завода
-го завода 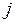 -му потребителю;
-му потребителю; 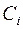 – полная себестоимость изготовления единицы продукции на
– полная себестоимость изготовления единицы продукции на 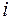 -ом заводе;
-ом заводе; 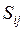 – транспортные расходы по доставке единицы продукции с
– транспортные расходы по доставке единицы продукции с 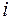 -го завода
-го завода 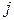 -му потребителю, р./шт.;
-му потребителю, р./шт.;
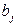 – потребность
– потребность 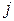 -го потребителя, тыс.шт.;
-го потребителя, тыс.шт.; 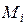 – объем выпуска продукции на
– объем выпуска продукции на 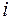 -ом заводе-изготовителе, тыс.шт.
-ом заводе-изготовителе, тыс.шт.
Требуется определить величины Xij – размеры поставок продукции заводов-изготовителей потребителям, при которых были бы минимальные совокупные производственные и транспортные затраты по всему объему перевозимой продукции.
Ограничение (4.3) означает, что потребность любого 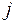 -го завода должна быть полностью удовлетворена. Ограничение (4.4) характеризует объем выпущенной продукции любого
-го завода должна быть полностью удовлетворена. Ограничение (4.4) характеризует объем выпущенной продукции любого 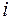 -го завода-изготовителя, который должен быть полностью распределен между всеми потребителями. Ограничение (4.5) показывает, что объем перевозок не может быть величиной отрицательной. Ограничение (4.6) свидетельствует о том, что решение задачи должно быть найдено исходя из того, что общий объем потребностей потребителей соответствует производственной мощности заводов-изготовителей.
-го завода-изготовителя, который должен быть полностью распределен между всеми потребителями. Ограничение (4.5) показывает, что объем перевозок не может быть величиной отрицательной. Ограничение (4.6) свидетельствует о том, что решение задачи должно быть найдено исходя из того, что общий объем потребностей потребителей соответствует производственной мощности заводов-изготовителей.
Указанная задача относится к закрытой (замкнутой) модели транспортной задачи, для которой справедливо равенство (4.6).
Если это равенство нарушатся, то либо суммарный объем производства всех заводов-изготовителей превышает суммарные заявки потребителей – неравенство (4.12), либо производственные мощности заводов-изготовителей недостаточны для удовлетворения заявок потребителей – неравенство (4.13). В обоих случаях задача представляет собой открытую модель транспортной задачи. Такие задачи могут быть сведены к задачам (4.1) – (4.6) введением либо фиктивного пункта потребления – в случае (4.12), либо фиктивного пункта производства – в случае (4.13).
Стоимость перевозок из фиктивного пункта производства (или в фиктивный пункт потребления) принимается равной нулю.
Вся исходная информация для построения экономико-математической модели систематизируется в виде табл. 4.1.
Таблица 4.1
Исходная информация для построения экономико-математической модели.
| Заводы-изготовители
| Объем выпускаемой продукции
тыс.шт. | Полная себестоимость единицы продукции, | Заводы-потребители | ||||
| … | 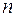
| ||||||
| Потребность | |||||||
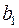
| 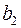
| 
| … | 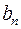
| |||
| Транспортные затраты | |||||||
| M1 | C1 | S11 | S12 | S13 | … | S1n | |
| M2 | C2 | S21 | S22 | S23 | … | S2n | |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
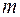
| Mm | Cm | Sm1 | Sm2 | Sm3 | … | Smn |
Для решения данной задачи, относящейся к классу так называемых «транспортных задач», могут быть использованы методы линейного программирования, обеспечивающих различную степень оптимизации плана перевозок: метод потенциалов, метод северо-западного угла, метод минимального элемента и др.
При выполнении данной лабораторной работы может быть использован метод минимального элемента или метод северо-западного угла.
Сущность метода минимального элемента состоит в следующем. Строится матрица совокупных затрат Cij, каждый элемент которой, определяется по формуле (4.2). В матрице Cij, начиная с самого минимального значения Cij из всех имеющихся, определяется объем перевозок Xij по формуле
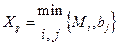 (4.14)
(4.14)
На каждой последующей итерации по мере возрастания численного значения элемента Cij величина Xij равняется минимуму из оставшегося нераспределенным объема производства на i-ом заводе-изготовителе и неудовлетворенной части заявки j-го потребителя.
Сущность метода северо-западного угла состоит в следующем: так же, как и а методе минимального элемента, сначала строится матрица совокупных затрат Cij. В этой матрице определяются объемы перевозок Xij по формуле (4.13), начиная с элемента С11 и далее по всей первой строке, т. е. для С12, С13, …, С1n, последовательно переходя ко второй строке, третьей и т. д.
На каждой последующей итерации величина Xij так же, как при методе минимального элемента принимается равной минимальному значению из оставшегося нераспределенным объема производства на i-ом заводе-изготови-теле и неудовлетворенной еще части заявки j-го потребителя.
Поскольку время лабораторной работы ограничено, студенты ориентировочно определяют четыре варианта плана закрепления потребителей за поставщиками. Пользуясь указанным преподавателем методом ручного счета (минимального элемента или северо-западного угла), студенты рассчитывают пятый вариант плана. Для всех возможных вариантов рассчитывается на ЭВМ значение целевой функции.
Лабораторная работа выполняется поэтапно.
1. Выписать исходную информацию и оставить экономико-матема-тическую модель задачи (см. выше);
2. Составить матрицу совокупных затрат Cij (табл. 4.2)
Таблица 4.2
Матрица совокупных затрат Cij
| Заводы-изготовители | Совокупные затраты Cij, р./шт. | ||||||
| … | 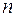
| ||||||
| С11 | С12 | С13 | С14 | С15 | … | C1n | |
| С21 | С22 | С23 | С24 | С25 | … | C2n | |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| Сm1 | Сm2 | Сm3 | Сm4 | Сm5 | … | Cmn |
3. Разработать четыре ориентировочных варианта плана закрепления потребителей за заводами-изготовителями (по форме табл.4.3);
4. Определить пятый расчетный план решения задачи, используя один из приведенных выше методов;
Таблица 4.3
Вариант плана закрепления потребителей за изготовителями
| Заводы-изготовители |
| Потребность | ||||||
| Распределение объемов выпуска потребителям, тыс. шт. | ||||||||
Используя ЭВМ [3,4] находят последовательно пять значений целевой функции рассматриваемой экономико-математической модели;
Производят анализ результатов. Оптимальным считается вариант плана закрепления потребителей за заводами-изготовителями, обеспечивающий минимальные затраты, связанные с изготовлением и транспортировкой по всему объему продукции. Варианты исходных данных, необходимых для выполнения работы представлены в табл. 4.4, 4.5.
Таблица 4.4
Исходные данные для первого варианта
| Заводы – изготовители
| Объем выпускаемой продукции
тыс.шт. | Полная себестоимость единицы продукции, | Заводы-потребители | |||||||
| Потребность | ||||||||||
| Транспортные затраты | ||||||||||
Таблица 4.5
Исходные данные для второго варианта
| Заводы-изгото-вители
| Объем выпускаемой проду-кции
тыс. шт | Полная себестоимость единицы продукции, | Заводы-потребители | ||||||
| Потребность | |||||||||
| Транспортные затраты | |||||||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
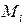 ,
,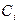 , р./шт.
, р./шт.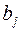 , тыс.шт.
, тыс.шт.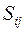 , р./шт.
, р./шт.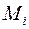 , тыс. шт.
, тыс. шт.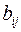 , тыс. шт.
, тыс. шт.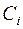 , р./шт.
, р./шт.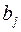 , тыс.шт.
, тыс.шт.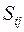 , р./шт.
, р./шт.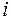
 , тыс.шт.
, тыс.шт.