СООТВЕТСТВИЯ МЕЖДУ МНОЖЕСТВАМИ

Лекция 6

СООТВЕТСТВИЯ МЕЖДУ МНОЖЕСТВАМИ

В начальном курсе математики встречаются различные взаимосвязи между множествами. Поэтому учителю следует понимать их сущность.

1. Найти значение выражений

а) (17 -1) : 4 б) (12 + 18) : (4 – 4) в) 2 · 7 + 6

2. Найти площадь фигуры:

F₁

F₂

F₂

3. Решить уравнение: у₁) 2 + х = 6 у₂) х – 7 = 1 у₃) 2х = 16

В первом случае устанавливали соответствие между заданными выражениями и их числовыми значениями, во втором - между фигурами и числами – значениями их площади, в третьем случае между уравнениями и их решением.

Выполняя упражнения, мы устанавливаем связь между элементами множеств. Эту связь можно предоставить либо в виде графов, либо в виде пар.

1. а • • 4 2. F₁ • • 4 3. У₁ • • 4

б • • 10 F₂ • • 10 У₂ • • 8

в• • 20 F₃ • У₃•

1.{(а 4); (в 20)} 2. {(F₁ 4); (F₂ 10); (F₃ 10)} 3. {(у₁ 4); (у₂ 8); (у₃ 8)}

Опред. Соответствием между множествами х и у называют всякое подмножество декартового произведения этих множеств.

Обозначения соответствий: Р; S; Т; S; S 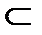х + у

Способы задания соответствия: перечислением всех пар, указание характеристического свойства этого подмножества, с помощью графа и с помощью графика.

Х = {1; 2; 4; 6}

У = {3; 5} а < в, гдеа 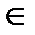х; в 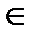у 5 • • • • График 1

•

3 • • •

•

• • • • • •

1 2 4 6

Иногда приходится рассматривать обратные отношения.

Опред. Пусть S – соответствие между множествами Х и У. Соответствие S^-1 между множествами У и Х называют обратным данному, если УS^-1Х <=> ХSУ

S и S^-1 – взаимно обратные соответствия • •

Пусть S = {(4; 2); (5; 3); (8; 6)} •

Тогда S^-1={(2; 4); (3; 5); (6; 8)} 6 • •

Графики S и S^-1 симметричным • •

относительно биссектрисы I и II координатных углов. • •

3 • •

2 • •

•

• • • • • • • •

4 5 8

Опред. Функциональным соответствием между множествами У и Х называют такое соответствие, при котором каждому элементу из множества Х сопоставляется не более одного элемента из множества У.

См. график 1 1 • •3

2 • не является функциональным

3 •

4 • •5

Опред. Если в функциональном соответствии каждому элементу Х соответствует единственный элемента из множества У, то такое соответствие называется отображением множества Хво множество У.

Опред. Взаимно-однозначным соответствием между множествами Х и У называют такое соответствие, при котором каждому элементу множества Х соответствует единственный элемент множества У и каждый элемент множества У соответствует только элементу множества Х.

12 Следующая ⇒