
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Многочлены. Действия с многочленами.
Руководство по решению задач к занятию 2.
Многочлены. Действия с многочленами.
1. Одночлен и действия с многочленами
Одночленом называется выражение, в котором числа и буквы связаны только двумя действиями – умножением и возведением в степень с натуральным показателем.
Пример 1.
1. -a  b;
b;
2. 17ax  bc;
bc;
3.  x
x  yz;
yz;
4. 3x  7y
7y  (-2y).
(-2y).
В этом примере многочлены 1), 2) и 3) записаны в стандартном виде, т.е. первый сомножитель – число, называемое коэффициентом одночлена, и каждый буквенный сомножитель входит в одночлен только один раз.
Приведем одночлен 4) к стандартному виду:
3x  7y
7y  (-2y)=3
(-2y)=3  7
7  (-2)
(-2)  x
x 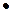 y
y 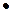 y= -42xy
y= -42xy 
Чтобы умножить одночлен на одночлен, нужно перемножить их коэффициенты и степени с одинаковыми основаниями.
Пример 2.Привести одночлен к стандартному виду.
7x  y
y 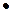 (-3x
(-3x 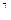 y
y 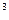 ) = 7
) = 7 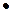 (-3) x
(-3) x  x
x 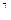 y y
y y 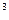 = -21x
= -21x 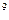 y
y 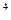 .
.
Пример 3.Перемножить одночлены -5x  t
t 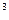 a и
a и 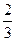 x
x 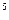 tb.
tb.
-5x  t
t 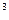 a
a 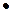 (
( 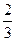 x
x 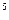 tb) = (-5)
tb) = (-5) 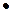
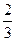 x
x  x
x 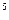 t
t 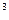 tab = -
tab = - 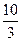 x
x 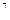 t
t 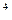 ab
ab
Многочленом называется сумма нескольких одночленов.
Одночлены, из которых состоит многочлен, называются членами многочлена.
Пример 4.
1) 2x 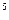 +3axy+b;
+3axy+b;
2) a+b
3) 5+x
4) 17x 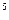 y
y 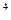 z
z 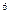
2. Приведение подобных слагаемых
Одночлены называются подобными, если, записанные в стандартном виде, они одинаковы или различаются лишь коэффициентами.
Пример 1.1)Одночлен -3x  y подобен одночлену 5 x
y подобен одночлену 5 x  y, так как буквенные сомножители у них одинаковые;
y, так как буквенные сомножители у них одинаковые;
2) ab  t подобен
t подобен 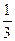 b
b  at
at
3) 2x подобен 3x;
4) 51 подобен 137;
5) -7u  x
x 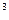 a
a 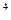 подобен 2a
подобен 2a 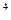 u
u  x
x 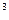 ;
;
6) одночлен 2x  y не подобен одночлену2xy
y не подобен одночлену2xy  , т.к. буквенные сомножители у них разные (они состоят из одних и тех же букв, но эти буквы возведены в разные степени).
, т.к. буквенные сомножители у них разные (они состоят из одних и тех же букв, но эти буквы возведены в разные степени).
Рассмотрим сумму подобных слагаемых:
3x  a – 2x
a – 2x  a + ax
a + ax 
Вынесем общий множитель за скобки:
x  a (3 – 2 + 1) = 2x
a (3 – 2 + 1) = 2x  a.
a.
эта операция называется приведением подобных членов.
3. Сложение и вычитание многочленов. Умножение многочленов
Многочлен, все члены которого являются одночленами стандартного вида, называется многочленом стандартного вида.
Сумму (разность) многочленов можно привести к многочлену стандартного вида. Для этого нужно раскрыть скобки и привести подобные члены.
При раскрытии скобок действует правило: если перед скобкой стоит знак “+”, то скобки опускаются, а знаки, стоящие внутри скобок, остаются прежними. Если же перед скобкой стоит знак “-”, то этот “минус” и скобки опускаются, знаки перед всеми членами многочлена меняются на противоположные.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|