Хелпикс

Главная

Контакты

Случайная статья



Методические рекомендации по выполнению контрольной работы по математике

Стр 1 из 2Следующая ⇒


Методические рекомендации по выполнению контрольной работы по математике

для студентов групп Э-1з, Д-1з

1. Пределы функции в точке и на бесконечности

1 Предел функции в точке

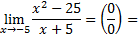
1)

 


Числитель и знаменатель дроби раскладывается на множители по формуле разности квадратов:

 

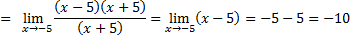
Ответ: −10

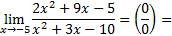
2)

 


Числитель и знаменатель дроби раскладывается на множители по формуле :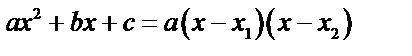

 


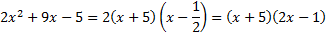
D = 81 – 4 · 2 · (−5) = 81 + 40 = 121

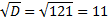
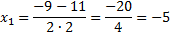
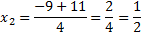
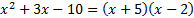
D = 9 – 4 · 1 · (−10) = 9 + 40 = 49

 

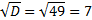
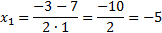
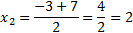
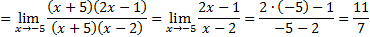
Ответ: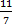

 

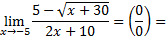
3)

 


Числитель и знаменатель дроби умножаем на выражение, сопряженное выражению с корнями (правило 2):

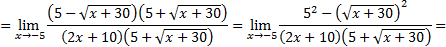
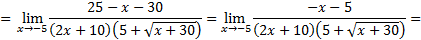
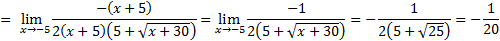
Ответ:

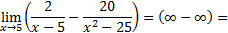
4)

 


Приводим дроби к наименьшему общему знаменателю:

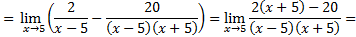
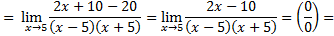
Числитель и знаменатель раскладываем на множители (правило 1):

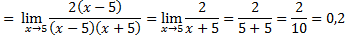
Ответ: 0,2

2 Предел функции на бесконечность

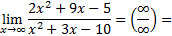
1)


Каждое слагаемое числителя и знаменателя дроби делим на x2 (правило 3):

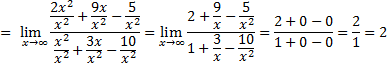
Ответ: 2

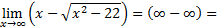
2)

 


Числитель и знаменатель дроби умножаем на выражение, сопряженное выражению с корнями (правило 2):

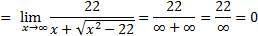
Ответ: 0

3. Замечательные пределы

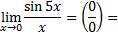
1)

 


Применяем I замечательный предел, умножаем числитель и знаменатель дроби на 5:

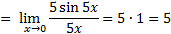
Ответ: 5

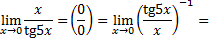
2)

 


Применяем I замечательный предел, умножаем числитель и знаменатель дроби на 5:

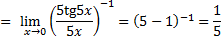
Ответ:

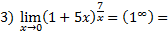
Применяем II замечательный предел:

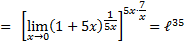
Ответ: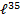

 

 

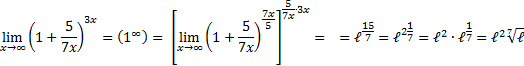
4)


Ответ: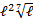

2. Нахождение производных сложных функций

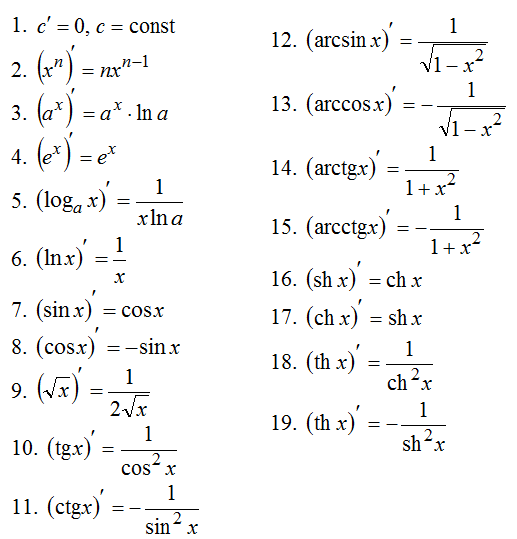
Производные элементарных функций Основные правила дифференцирования

Пример 1:

Найти производную функции:

а)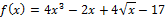  

Вычисляем по правилу производной суммы (разность):

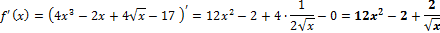
Ответ: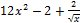

б)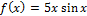

Вычисляем по правилу производной произведения:

 

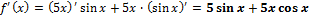
Ответ: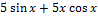

в)

Вычисляем по правилу производной частного:

 

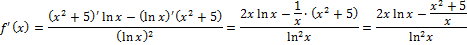
Это выражение можно преобразовать, тогда получим:

 

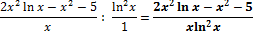
Ответ: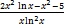

г) 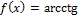10x

Вычисляем по правилу производной сложной функции, где arcctg □ - внешняя функция, а 10x – внутренняя:

 

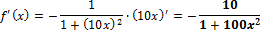
Ответ: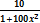

 

д)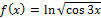

Вычисляем по правилу производной сложной функции. Здесь несколько функций, от каждой находим производную:

ln □              

              

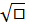
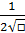
cos□               -sin□

3x                        3

Получаем:

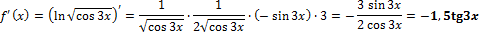
Ответ: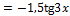

Пример 2

Составим уравнение касательной и нормали к графику функции 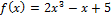 в точке с абсциссой

x0 = -2.

Выполняем по алгоритму:

1) f (x0) = 2 · (-2)3 – (-2) + 5 = 2 · (-8) + 2 + 5 = -16 + 2 + 5 = −9

2) f ′ (x) = (2x3 – x + 5)′ = 6x2 – 1

3) f ′(x0) = 6 · (-2)2 -1 = 6 · 4 – 1 = 24 – 1 = 23

Уравнение касательной (подставляем):

y = f (x0) + f ′ (x0) · (x – x0)

y = −9 + 23(x + 2)

y = 9 + 23x + 46


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.