
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
lim x→∞ (kf(x))=kb.
lim x→∞ (kf(x))=kb.
Правило 1. Для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на х в старшей степени.
Пример 1.
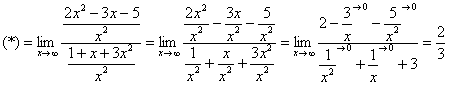
Пример 2
Найти предел 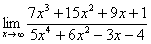
Пределы с неопределенностью вида и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!».
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 3
Решить предел 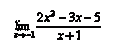
Сначала попробуем подставить -1 в дробь: 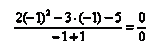
В данном случае получена так называемая неопределенность 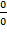
Правило 2.: Если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 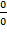 , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения
Вычислим предел заданной функции: Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
2х2 -3х-5=0
Сначала находим дискриминант: 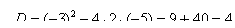
И квадратный корень из него: 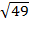 =7; далее находим корни:
=7; далее находим корни: 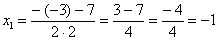
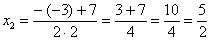
Таким образом, 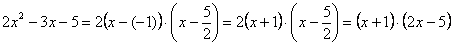
Числитель на множители разложен.
Знаменатель. Знаменатель х+1 уже является простейшим множителем, и упростить его никак нельзя.
Сокращаем числитель и знаменатель на множитель х+1, и подставляем в оставшееся выражение х= -1; получаем 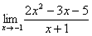 = -7
= -7
Самостоятельно: вычислить предел функции 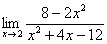
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|