Сначала находим определитель матрицы.

1) Сначала находим определитель матрицы.

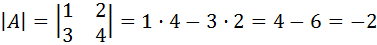
2) Находим матрицу миноров .

Матрица миноров имеет такие же размеры, как и матрица 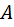, то есть в данном случае .
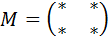Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице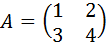
Сначала рассмотрим левый верхний элемент

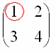
Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

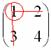
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:

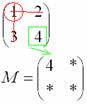
Рассматриваем следующий элемент матрицы :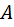

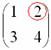
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:

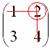
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:

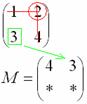
Аналогично рассматриваем элементы второй строки и находим их миноры:

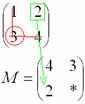
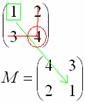
Готово.

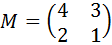– матрица миноров соответствующих элементов матрицы .

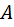3) Находим матрицу алгебраических дополнений .

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:

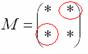
Именно у этих чисел, которые я обвел в кружок!

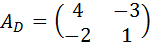– матрица алгебраических дополнений соответствующих элементов матрицы .

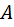4) Находим транспонированную матрицу алгебраических дополнений .

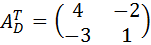– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

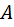5) Ответ.

Вспоминаем нашу формулу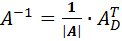
Всё найдено!

Таким образом, обратная матрица: .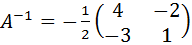

Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Как проверить решение?
Необходимо выполнить матричное умножение 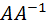либо .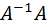

Проверка:

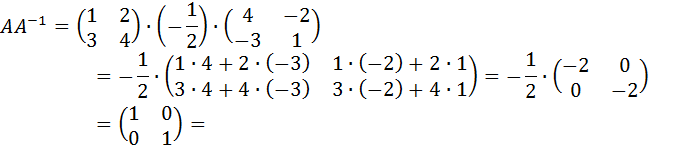
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).

Таким образом, обратная матрица найдена правильно.

⇐ Предыдущая 12