Показатели вариации

⇐ ПредыдущаяСтр 3 из 3

Показатели вариации

1. По исходным данным (n=50):

Подготовительные расчёты:

- (x_1-x)+(x₂-x)+…(x_n-x) = 0

- |x_1-x|+|x₂-x|+…|x_n-x| = (примерно) 99,962

- (x_1-x)ˆ2+(x₂-x)ˆ2+…(x_n-x)ˆ2 = (примерно) 331,594

- (x_1-x)ˆ3+(x₂-x)ˆ3+…(x_n-x)ˆ3 = (примерно) 1064,238

- (x_1-x)ˆ4+(x₂-x)ˆ4+…(x_n-x)ˆ4 = (примерно) 8491,410

1) Дисперсия:

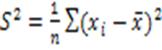
= (примерно) 6,632

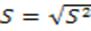2) Среднее квадратное отклонение:

= (примерно) 2,575

3) Среднее линейное отклонение:

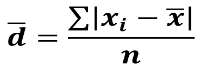= (примерно) 1,999

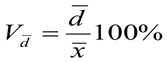4) Коэффициент линейной вариации:

= (примерно) 2,627%

5) Коэффициент осцилляции:

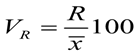
= (примерно) 13,888%

6) Правило 3-ёх сигм:

(x-3*S) = (примерно) 68,381
(x+3*S) = (примерно) 83,832

68,381< N < 83,832

(для всех значений верно)

7) Коэффициент вариации:

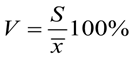
= (примерно) 3,384%

8) Квартильный показатель вариации Гальтона:

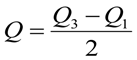
= 1,42

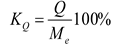9) Относительный квартильный показатель вариации:
= (примерно) 1,886%

10) Центральный момент первого порядка:

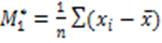
= 0

11) Центральный момент второго порядка:

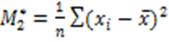
= S² = (примерно) 6,632

12) Центральный момент третьего порядка:

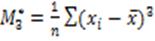
= (примерно) 21,285

13) Центральный момент четвёртого порядка:

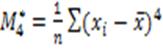
= (примерно) 169,828

14) Коэффициент асимметрии:

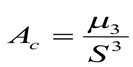
= (примерно) 1,246

15) Коэффициент эксцесса:

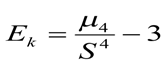
= (примерно) 0,861

2. По интервальному ряду (n=50):

Предварительные расчёты:

- (x₁-x)*m₁ + (x₂-x)*m₂ +…(x₈-x)*m₈= 0

- |x₁-x|*m₁ + |x₂-x|*m₂ +… |x₈- x|*m₈= (примерно) 102,005

- (x₁-x)²*m₁+(x₂-x)² *m₂+...(x₈-x)² *m_{8 =}(примерно) 360,848

- (x₁-x)⁴*m₁+(x₂-x)³ *m₂+...(x₈-x)³ *m₈₌(примерно) 1230,901

- (x₁-x)⁴*m₁+(x₂-x)⁴*m₂+...(x₈-x)⁴*m₌(примерно) 10918,897.

1) Дисперсия:

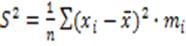= (примерно) 7,217

2) Среднее квадратное отклонение:

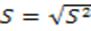= (примерно) 2,686

3) Среднее линейное отклонение:

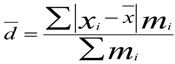
= (примерно) 2,040

4) Коэффициент линейной вариации:

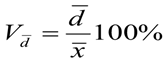
= (примерно) 2,683%

5) Коэффициент осцилляции:

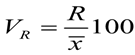
= (примерно) 13,902%

6) Правило 3-ёх сигм:

(x-3*S) = (примерно) 67,972

(x+3*S) = (примерно) 84,091

67,972 < N < 84,091

(для абсолютного большинства значений верно)

6) Коэффициент вариации:

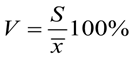
= (примерно) 3,533%

7) Квартильный показатель вариации Гальтона:

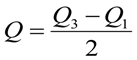
= (примерно) 1,417

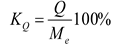8) Относительный квартильный показатель вариации:
= (примерно) 1,880%

9) Центральный момент первого порядка:

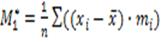= 0

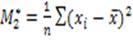10) Центральный момент второго порядка:

= S² = (примерно) 7,217

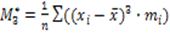11) Центральный момент третьего порядка:

= (примерно) 24,618

12) Центральный момент четвёртого порядка:

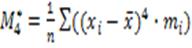
= (примерно) 218,378

13) Коэффициент асимметрии:

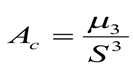
= (примерно) 1,270

15) Коэффициент эксцесса:

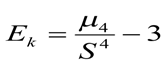
= (примерно) 1,193

Выводы

1) Данные – вторичные, одномерные, пространственные, количественные непрерывные;

2) Получилось 8 интервалов из 50 наблюдений;

3) И по исходным данным, и по интервальному ряду распределения x = Me = Mo (на самом деле x> Me> Mo, что в свою очередь указывает на правостороннюю асимметричность распределения);

4) Около 25% значений выборки меньше 74,09, около 25% значений больше 74,09 и меньше 75,04, около 25% значений больше 75,04 и меньше 76,91, около 25% значений больше 76,91;

5) Около 10% значений меньше 73,6, и около 10% значений больше 80,2;

6) В среднем отклонение от среднего значения составляет около 2,5% (линейное отклонение – около 2%, но корень из дисперсии реагирует на вариацию более чутко);

7) Значения исследуемого признака в данной совокупности распределены по закону нормального распределения;

8) Коэффициент вариации менее 3,5%, что меньше 10%. Значит, вариация значений совокупности незначительна;

9)Колебание крайних значений вокруг средней составляет около 13,9%;

10.1) Коэффициент асимметрии составляет около 1,25. Значит, что данный ряд ассиметричен и имеет правостороннюю асимметрию (цент сдвинут влево);

10.2) Коэффициент эксцесса составил около 1, что свидетельствует о приближенности графика распределения значений к островершинному;

Доказательство пункта 10):

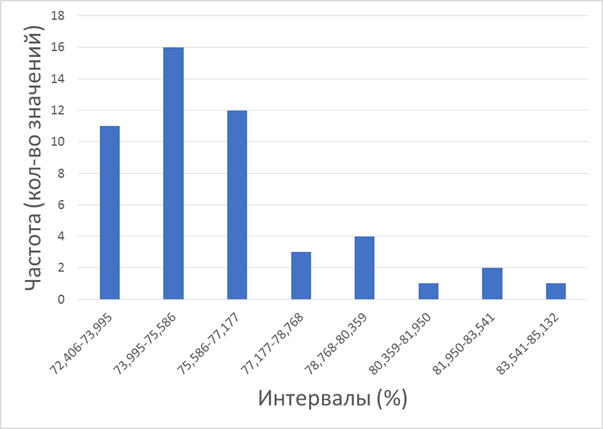
Рис. 1 Распределение частот значений показателя процента выигранной первой подачи 50-ти игроков рейтинга ATP в 2018 г. по интервалам.

(кол-во значений, входящих в интервал)

Источник: данные выборочного обследования.

11) Значения показателей по исходным данным и интервальному ряду в определённой степени различаются в силу раздвигания границ первоначального массива интервалами, искусственного увеличения ими количества значений и усреднения значений всех наблюдений по отношению к частоте. Значит, при использовании интервального ряда присутствует погрешность (которая, как было заметно, стремительно увеличивается при возведении значений в натуральную степень), то есть по возможности лучше использовать исходные данные (для более точных вычислений).

⇐ Предыдущая 1 23