Показательные уравнения. Логарифмические уравнения

Показательные уравнения. Логарифмические уравнения

Напомним, что показательным называется уравнение, содержащее переменные только в показателе степени.

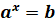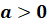Уравнение , где и 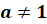, называется простейшим показательным.

Если 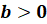, то уравнение имеет единственное решение .

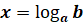Если 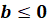, то уравнение не имеет корней.

Решение показательных уравнений основано на свойстве степеней: две степени с одним и тем же положительным и отличным от единицы основанием равны тогда и только тогда, когда равны их показатели.

Давайте рассмотрим некоторые виды показательных уравнений и методы их решения.

1. Приведение обеих частей уравнения к одному основанию .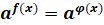

Полученное уравнение пр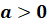и и 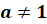равносильно уравнению .

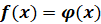Уравнение вида 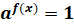, при 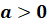, 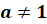равносильно уравнению 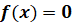, так как .

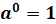Решите уравнение .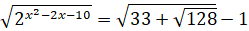

Решение.

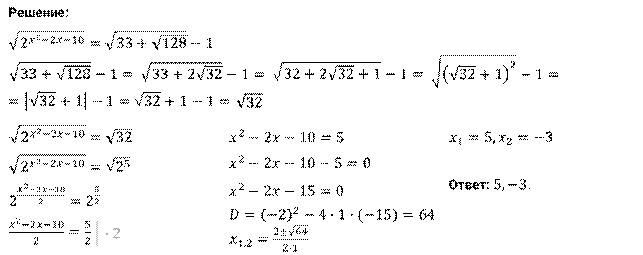
2. Вынесение общего множителя за скобки в уравнениях, в левой части которых записана сумма или разность степеней с одним основанием.

Например, .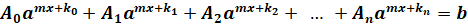

Причём, если 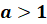, выносится степень с меньшим показателем, если 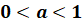, – степень с большим показателем.

Решите уравнение . .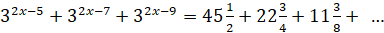

Решение.

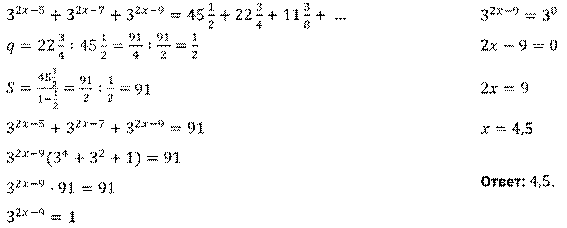
3. Уравнения вида

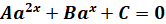где 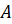, , 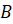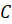– некоторые числа, причём 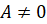, 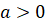и 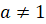, сводятся к решению квадратного уравнения 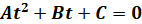(или уравнения более высокой степени) при помощи замены 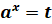при .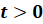

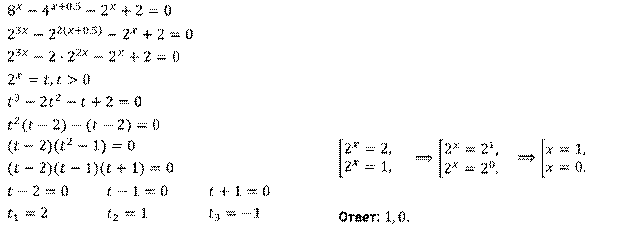
Решите уравнение .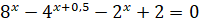

Решение.

А теперь перейдём к логарифмическим уравнениям. Напомним, что логарифмическим называется уравнение, содержащее переменные только под знаком логарифма.

Давайте рассмотрим основные виды логарифмических уравнений и методы их решения.

12 Следующая ⇒