
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение систем уравнений и неравенств»
22.05.2020
«Решение систем уравнений и неравенств»
Задание1. Пройдите по ссылке и посмотрите урок по теме «Решение систем уравнений и неравенств» https://vk.com/away.php?to=https%3A%2F%2Fyandex.ru%2Fvideo%2Fpreview%2F%3FfilmId%3D10871118717851833052%26text%3Dj%252Cobt%2Bvtnjls%2Bhtitybz%2Bcbcntv%2Behfdytybq%2Bb%2Bythfdtycnd%2B11%2Brkfcc&post=-193120823_129&cc_key=
Задание 2. Рассмотрите еще три примера решения систем уравнений и неравенств

3. Решите систему неравенств

Вариант 1
1.Найдите значение выражения 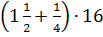 .
.
а) 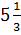 ; б) 28; в) 14; г) 32.
; б) 28; в) 14; г) 32.
2.Представьте в виде десятичной дроби число 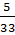 .
.
а) 1,(5); б) 0,1 (15); в) 0,155; г) 0,(15).
3.Даны комплексные числа z1= -5 + 4i и z2= 1 + 2i. Найдите z1 - z2.
а) -4 + 2i; б) -6 + 2i; в) 6 - 2i; г) 4 - 2i.
4.Вычислите 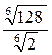 .
.
а) 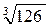 ; б) 8; в) 2; г) 3.
; б) 8; в) 2; г) 3.
5.Вычислите 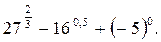
а) 6; б) 12; в) 7; г) 8.
6.Упростите выражение: 7∙log554.
а) 35; б) 28; в) 4375; г) 2401.
7.Решите уравнение 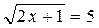 .
.
а) 4; б) 2; в) 13; г) 12.
8.Решите уравнение 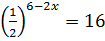 .
.
а) -5; б) 1; в) 5; г) -1.
9.Решите уравнение log2 (x+6)=3.
а) 0; б) 2; в) 14; г) 3.
10.Решите неравенство 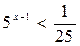 .
.
а) (-∞; 3); б) (-∞; 1); в) (-∞; -1); г) [-1; +∞).
11.В чемпионате по гимнастике участвуют 40 спортсменок: 17 из России, 13 из США, остальные из Китая. Порядок их выступления определяется жребием. Найдите вероятность того, что первой будет выступать спортсменка из Китая.
а) 0,125; б) 0,75; в) 0, 5; г) 0,25.
12.Даны векторы 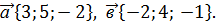
Найдите координаты вектора 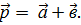
а) 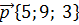 ;
;  б)
б) 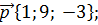 в)
в) 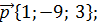 г)
г) 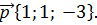
13.Упростите выражение 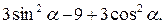
а) -3; б) -6; в) -8; г) 0.
14.Решите уравнение 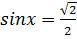 .
.
а) 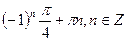 ; б)
; б) 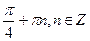 ;
;
в) 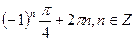 ; г)
; г) 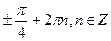 .
.
15.Стороны основания прямоугольного параллелепипеда равны 8 см и 5 см. Объем его равен 120 см3. Найдите высоту этого параллелепипеда.
а) 4 см;  б) 6 см; в) 8 см; г) 3 см.
б) 6 см; в) 8 см; г) 3 см.
16.Радиус основания конуса равен 2 см, а его высота - 6см. Найдите объем этого конуса.
а) 24p см3  ; б) 72p см3; в) 8 см3; г) 8p см3.
; б) 72p см3; в) 8 см3; г) 8p см3.
17.Найдите производную функции y = 3cos x + x2.
а) y ' = -3sin x + 2x; б) y ' = 3sin x -2х; в) y ' = 4x - sin x; г) y ' = x2 + 2cos x.
18.Найдите все первообразные функции f(x) = 6x2 - 2.
а) F(x) = 2x3 – 2; б) F(x) = 2x3 – 2х +С;
в) F(x) = 12x + C; г) F(x) =  x3 - x +C .
x3 - x +C .
19.Решите уравнение 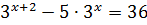
а) 2; б) 12; в) 3; г) -2.
20. Установите соответствие между указанным телом вращения и его характеристиками:
| 1. Цилиндр | А) осевым сечением является прямоугольник |
| 2. Конус | Б) осевым сечением является трапеция |
| 3. Усеченный конус | В) осевым сечением является круг |
| 4. Сфера | Г) осевым сечением является равнобедренный треугольник |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|