
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лабораторная работа №17. ИЗУЧЕНИЕ ДВИЖЕНИЯ МАЯТНИКА МАКСВЕЛЛА. ВВЕДЕНИЕ
Министерство образования Российской Федерации
Тверской государственный университет
Кафедра общей физики
Лаборатория механики
Лабораторная работа №17
ИЗУЧЕНИЕ ДВИЖЕНИЯ МАЯТНИКА МАКСВЕЛЛА
Тверь
Цель работы: ознакомление со сложным движением твердого тела на примере движения маятника Максвелла.
Приборы и принадлежности:маятник Максвелла ,сменные кольца, штангенциркуль.
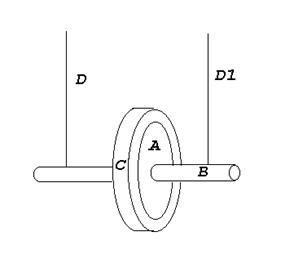
ВВЕДЕНИЕ
Маятник Максвелла (см. рис.1) представляет собой однородный металлический диск А, в середине которого укреплен металлический стержень В. На диск одевается сменное кольцо С. К концам стержня прикреплены две крепкие капроновые нити Д и Д 1. Они тщательно, виток к витку, наматываются на стержень от концов к диску. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень и, следовательно, к подъему маятника. Движение маятника после этого замедляется, маятник останавливается и снова начинает свое движение вниз и т.д. Расстояние, проходимое маятником, измеряется по вертикальной линейке с делениями. Уравнения движения маятника без учета сил трения имеют вид:
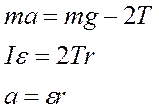 (1)
(1)
(2)
(3)
 При записи уравнений (1) и (2) учтено, что сложное движение твердого тела можно рассматривать как суперпозицию поступательного движения центра масс и вращательного движения относительно мгновенной оси, проходящей через центр масс.
При записи уравнений (1) и (2) учтено, что сложное движение твердого тела можно рассматривать как суперпозицию поступательного движения центра масс и вращательного движения относительно мгновенной оси, проходящей через центр масс.
Рис.1
В соотношениях (1)–(3) 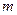 - масса маятника,
- масса маятника,  - момент инерции маятника,
- момент инерции маятника, 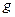 - ускорение силы тяжести,
- ускорение силы тяжести, 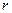 - радиус стержня,
- радиус стержня, 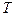 -натяжение одной нити,
-натяжение одной нити,  - ускорение поступательного движения центра масс маятника,
- ускорение поступательного движения центра масс маятника, 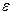 - угловое ускорение маятника.
- угловое ускорение маятника.
Ускорение  может быть найдено по измеренному времени движения t и проходимому маятником расстоянию S из уравнения
может быть найдено по измеренному времени движения t и проходимому маятником расстоянию S из уравнения
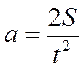 , (4)
, (4)
которое является следствием соотношений (1)-(3) .
Уравнения (1)-(3) дают
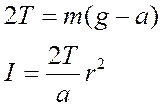 (5)
(5)
(6)
Пользуясь этими выражениями, определяют момент инерции маятника Максвелла. Натяжение нитей при движении маятника можно вычислить из уравнения (1), зная 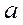 . Момент инерции
. Момент инерции  маятника Максвелла можно также вычислить, задаваясь геометрическими размерами и массой отдельных частей
маятника Максвелла можно также вычислить, задаваясь геометрическими размерами и массой отдельных частей
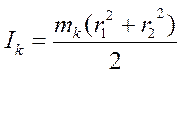
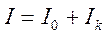 (7)
(7)
(8) 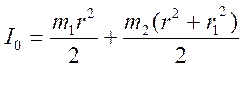 (9)
(9)
 где
где  - момент инерции диска А со стержнем В,
- момент инерции диска А со стержнем В, 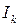 - момент инерции съемного кольца;
- момент инерции съемного кольца;
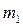 ,
, 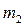 ,
, 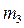 -массы стержня, диска и кольца,
-массы стержня, диска и кольца, 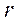 - радиус стержня,
- радиус стержня,  - радиус диска,
- радиус диска, 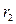 -наружный радиус кольца.
-наружный радиус кольца.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|