Иррациональные и показательные уравнения.

Иррациональные и показательные уравнения.

Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.

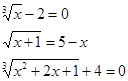Например:

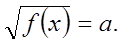Методы решения иррациональных уравнений.

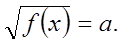Если а <0 (отрицательно), то уравнение - НЕ имеет решений.

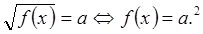Если а ≥0, то уравнение

Это следует из определения арифметического корня.

Пример.

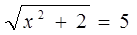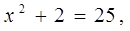Т.к. 5>0, следовательно, уравнение имеет решение, возводим в квадрат левую и правую части уравнения:

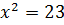
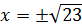
Ответ: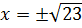

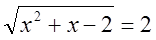Т.к. 2>0, уравнение имеет решение. Возводим обе части уравнения в квадрат.

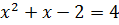
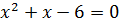
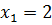
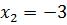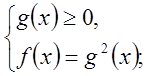2. Решение иррациональных уравнений, используя переход к смешанной системе.

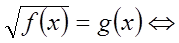
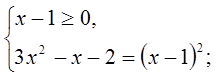
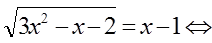Пример.

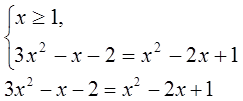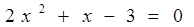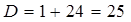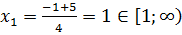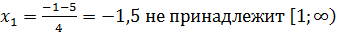, следовательно, x=-1,5 – не корень.

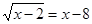Например.

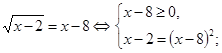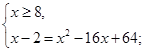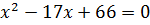
D=25

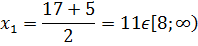
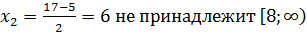, значит x=6 – не корень.

Ответ: x=11.

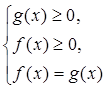3. Переход к равносильной системе.

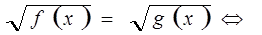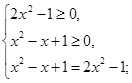
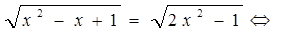Например.

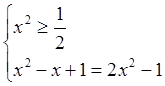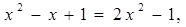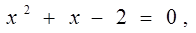
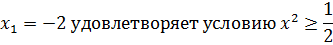
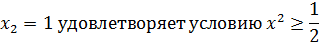
Ответ: -2,1.

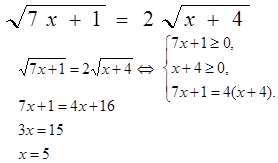Ответ: x=5

Показательные уравнения.

Показательным называется уравнение, содержащее неизвестную переменную в показателе степени.

Примеры показательных уравнений:

5^х+2= 125

3^х·2^х= 8^х+3

3^2х+4·3^х-5 = 0

Основными методами решения показательных уравнений являются:

Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:

Теорема 1. Показательное уравнение a^f^(x)= a^g^(x)(где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).