
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Директрисы фигуры эллипс. Гипербола и ее свойства
Директрисы фигуры эллипс
С фигурой эллипс связаны две прямые, называемые директрисами. Их уравнения:
x = a / e ; x = - a / e .
Теорема.Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением : 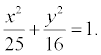
• Координаты нижней вершины: x = 0; y2 = 16; y = -4.
• Координаты левого фокуса: c2 = a 2 – b2 = 25 – 16 = 9; c = 3; F2 (-3; 0).
• Уравнение прямой, проходящей через две точки:
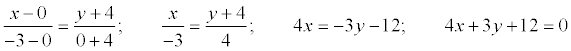
Пример. Составить уравнение границы фигуры эллипс, если его фокусы F 1 (0; 0), F2 (1; 1), большая ось равна 2.
Уравнение границы имеет вид: 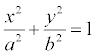 . Расстояние между фокусами:
. Расстояние между фокусами:
2 c = 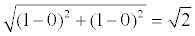 , таким образом, a2 – b2 = c2 = 1/2
, таким образом, a2 – b2 = c2 = 1/2
по условию 2а = 2, следовательно а = 1, b = 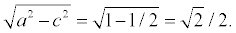
Итого искомое уравнение имеет вид: 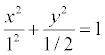 .
.
Гипербола и ее свойства
Определение. Гиперболойназывается множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемыхфокусамиесть величина постоянная, меньшая расстояния между фокусами.
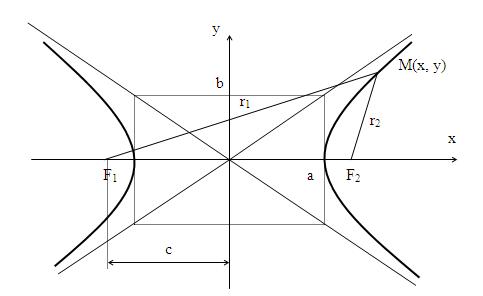
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
Выберем на гиперболе произвольную точку М(х, у). Тогда :
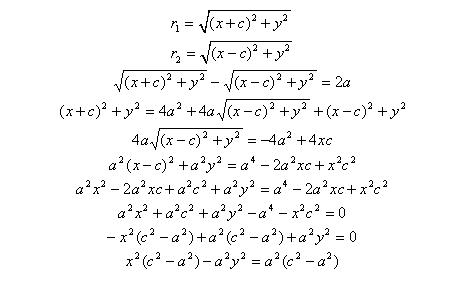
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
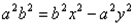
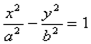
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола имеет две асимптоты, уравнения которых 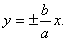
Определение.Отношение 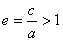 называется эксцентриситетомгиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетомгиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а 2 = b2
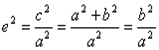 :
:
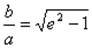
Если а = b , e = 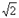 , то гипербола называется равнобочной (равносторонней).
, то гипербола называется равнобочной (равносторонней).
Определение.Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисамигиперболы. Их уравнения: 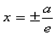
Теорема.Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
Доказательство.Изобразим схематично гиперболу.
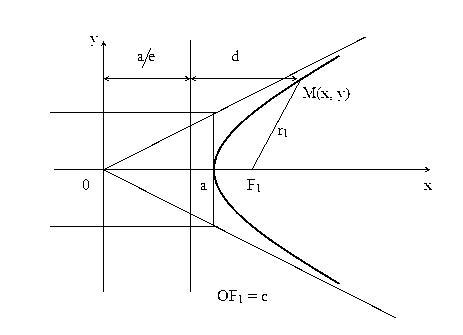
Из очевидных геометрических соотношений можно записать:
a / e + d = x , следовательно d = x – a / e .
( x – c ) 2 + y2 = r 2
Из канонического уравнения: 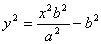 , с учетом b2 = c2 – a2:
, с учетом b2 = c2 – a2:
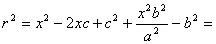
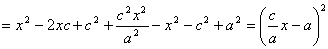
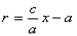
Тогда т.к. с/ a = e , то r = ex – a .
Итого: 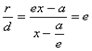
Для левой ветви доказательство аналогично. Теорема доказана
Пример 1. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 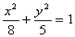
Для эллипса: c 2 = a2 – b2 .
Для гиперболы: c2 = a2 + b2 .
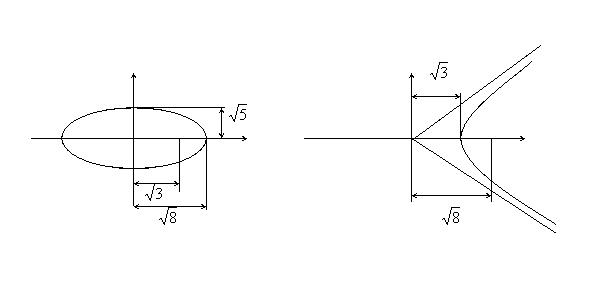
Уравнение гиперболы: 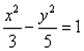
Пример 2. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 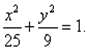
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a2 ; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 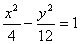 - искомое уравнение.
- искомое уравнение.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|