Билет 16,17. Чертеж фигуры эллипс. Эксцентриситет фигуры эллипс

Билет 16,17

Эллипс и его свойства

Определение. Эллипс -это геометрическая фигура, которая ограничена кривой, заданной уравнением .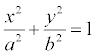

Он имеет два фокуса. Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Чертеж фигуры эллипс

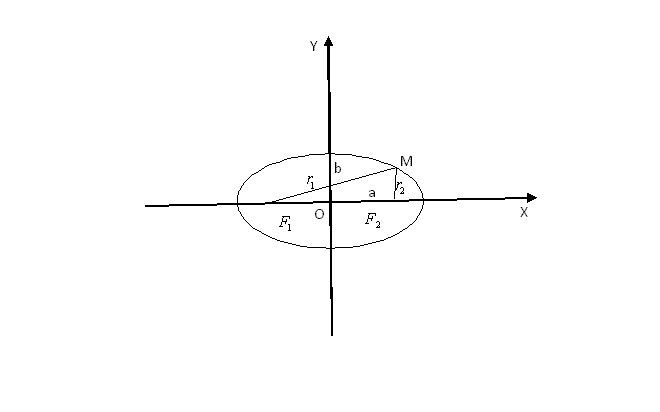
F₁ , F₂ – фокусы . F₁ = ( c ; 0); F ₂ (- c ; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема.Фокусное расстояние и полуоси связаны соотношением:

a² = b ² + c ².

Доказательство:В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2* (по теореме Пифагора). В случае, если точка М находится на пересечении его с горизонтальной осью, r₁ + r ₂ = a – c + a + c. Т.к. по определению сумма r₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a ² = b ² + c ²

r₁ + r₂ = 2 a .

Эксцентриситет фигуры эллипс

Определение.Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называетсяэксцентриситетом.

е = с/ a .

Т.к. с < a , то е < 1.

Определение.Величина k = b / a называется коэффициентом сжатия, а величина 1 – k = ( a – b )/ a называется сжатием.

Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e ² .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х ₁ , у ₁ ) выполняется условие: 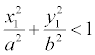, то она находится внутри эллипса, а если 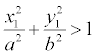, то точка находится вне его.

Теорема.Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения :

r ₁ = a – ex , r₂ = a + ex .

Доказательство.Выше было показано, что r₁ + r₂ = 2 a . Кроме того, из геометрических соображений можно записать:

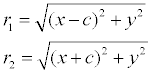
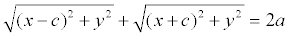
После возведения в квадрат и приведения подобных слагаемых:

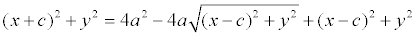
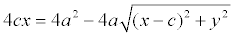
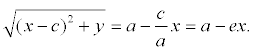
Аналогично доказывается, что r₂ = a + ex . Теорема доказана.

12 Следующая ⇒