Хелпикс

Главная

Контакты

Случайная статья



Тема урока: Уравнения и системы уравнений. Рациональные, иррациональные, показательные и логарифмические уравнения

Стр 1 из 2Следующая ⇒


Тема урока: "Уравнения и системы уравнений. Рациональные, иррациональные, показательные и логарифмические уравнения"

1.Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

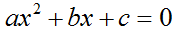
a, b и c - числа, х - переменная

Для нахождения корней квадратного уравнения необходимо найти дискриминант по формуле

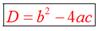
1) Если D>0, то уравнение имеет два корня, которые находятся по формулам

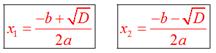
2) Если D=0, то уравнение имеет один корень, который находится по формуле

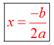
3) Если D<0, то уравнение не имеет корней.

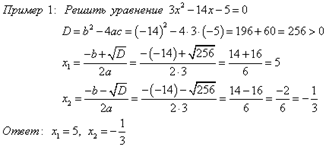
2.Решение показательных и логарифмических уравнений.

Показательными называются уравнения, в которых неизвестное содержится в показателе степени. Простейшее показательное уравнение имеет вид: ах = аb, где а> 0, а 1, х - неизвестное.

Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.

1. а0 = 1, а1= а.

2. аm/n= 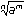, где m и n– натуральные числа.

3. a-n = 1/ аn

4. an × am = an+m

5. an/am = an-m

6. (an)m = an-m

7. (ab)n = an×bn

8. (a/b)n = an/bn.

При решении показательных уравнений пользуются также следующими свойствами показательной функции: y = ax, a > 0, a 1:

1. ax>0, при всех a>0 и x R;

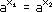
2. x1 =x2.

Для представления числа в виде степени используют основное логарифмическое тождество: b = 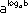, a > 0, a 1, b > 0.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.