
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Желаем успеха!. СПРАВОЧНЫЙ МАТЕРИАЛ
Желаем успеха!
СПРАВОЧНЫЙ МАТЕРИАЛ
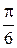
| 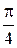
| 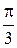
| 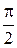
| ||
| sina | 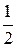
| 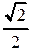
| 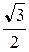
| ||
| cosa | 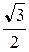
| 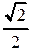
| 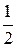
| ||
| tga | 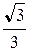
| 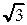
| не существует |
Формулы сложения:
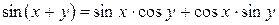
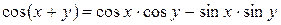
Формула перехода к новому основанию:
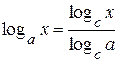 ,
,
( 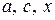 – положительные числа,
– положительные числа, 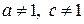 )
)
Производная сложной функции:
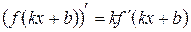
| Формулы площади треугольника: | |
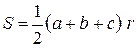
| 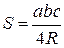
|
| ( | |
Площадь боковой поверхности конуса:
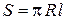
| Объем конуса:
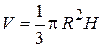
|
| ( | |
Площадь сферы:
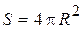 . .
| Объем шара:
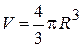 . .
|
ЧАСТЬ 1
| При выполнении заданий части 1 в бланке ответов №1 под номером выполняемого вами задания (А1 – А14) поставьте знак «´» в клеточку, номер которой соответствует номеру выбранного вами ответа. |
| A1 |
Вычислите: 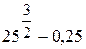 .
.
| 1) | 37,25 | 2) | 14,75 | 3) | 124,75 | 4) | 26,25 |
| A2 |
Упростите выражение  .
.
| 1) | 2) | – 5 | 3) | 4) | – 3 |
| A3 |
Упростите выражение 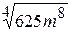 .
.
| 1) | 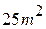
| 2) | 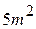
| 3) | 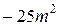
| 4) | 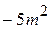
|
| A4 |
Найдите значение выражения 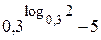 .
.
| 1) | – 4,91 | 2) | – 4,7 | 3) | – 4 | 4) | – 3 |
| A5 |
Укажите промежуток, содержащий корень уравнения 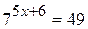 .
.
| 1) | 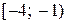
| 2) | 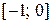
| 3) | (0; 2) | 4) | 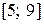
|
| A6 |
Какому промежутку принадлежит корень уравнения 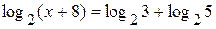 ?
?
| 1) | (-8; -5] | 2) | (-1; 3) | 3) | (3; 5) | 4) | [5; 8] |
| A7 |
Укажите график функции, возрастающей на отрезке [-3; 2].
| 1) | 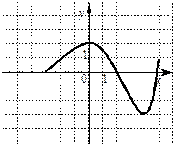
| 2) | 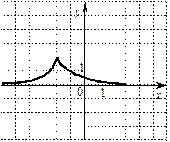
|
| 3) | 
| 4) | 
|
| A8 |
Укажите множество решений неравенства 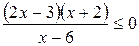 .
.
| 1) | 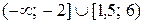
| 2) | 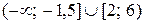
|
| 3) | 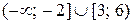
| 4) | 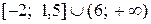
|
| A9 |
Вычислите значение производной функции у = sin x – 2х в точке х0 = 0.
| 1) | 2) | 3) | –3 | 4) | –1 |
| A10 |
Найдите область определения функции 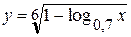 .
.
| 1) | [0,7; +¥) | 2) | (0; 0,7] | 3) | (–¥; 0,7] | 4) | (0,7; +¥) |
| A11 |
Найдите множество значений функции у = 6х –12.
| 1) | (0; +¥) | 2) | (–12; +¥) | 3) | [–12; +¥) | 4) | (–¥; – 12) |
| A12 |
Решите уравнение 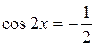 .
.
| 1) | 
| 2) | 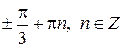
|
| 3) | 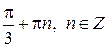
| 4) | 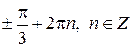
|
| A13 |
 На рисунке изображен график функции
На рисунке изображен график функции 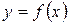 . Какому из следующих промежутков принадлежит корень уравнения
. Какому из следующих промежутков принадлежит корень уравнения 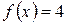 ?
?
| 1) | (– 6; –4) | 2) | (5; 7) |
| 3) | (– 2; 0) | 4) | (0; 2) |
| A14 |
Через точку графика функции у = ех – 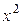 с абсциссой х0 = 1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.
с абсциссой х0 = 1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.
| 1) | e – 2 | 2) | – 1 | 3) | e – 1 | 4) | – 2 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
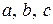 – стороны треугольника,
– стороны треугольника, 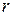 – радиус вписанной окружности,
– радиус вписанной окружности, 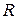 – радиус описанной окружности)
– радиус описанной окружности)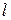 – длина образующей,
– длина образующей, 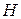 – высота)
– высота)