
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Организационная часть. Сообщение темы, цели и основных заданий. Актуализация опорных знаний и мотивация учебной деятельности. Лекция.. Метод приведения обеих частей неравенства к одному основанию.. Метод логарифмирования обеих частей неравенства.
1. Организационная часть
Поприветствовать студентов, отметить в журнале студентов, которые отсутствуют, проверить готовность аудитории и студентов к проведению занятия.
2. Сообщение темы, цели и основных заданий
3. Актуализация опорных знаний и мотивация учебной деятельности
1. Проверка домашнего задания.
2. Фронтальный опрос
2.1. Определение показательной функции.
2.2. Повторить свойства степени по таблице.
4.Лекция.
4.1. Метод приведения обеих частей неравенства к одному основанию.
Определение.Неравенства, содержащие переменную в показателе степени, называются показательными.
При решении показательных неравенств используются свойства показательной функции, свойства степени. Рассмотрим простейшие методы решения показательных неравенств.
а) 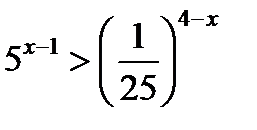
приведём обе части неравенства к одинаковым основаниям. Учитывая, что 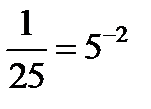 , то
, то 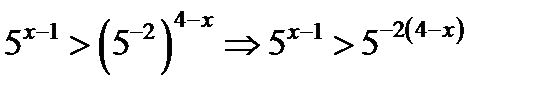 , т.к.
, т.к. 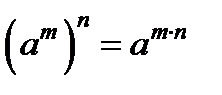 (свойство степени). Основание 5 > 1
(свойство степени). Основание 5 > 1 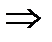 функция возрастающая и поэтому
функция возрастающая и поэтому 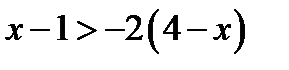 .
.
Решаем неравенство первой степени.
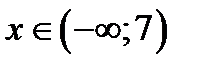

б)  . Приведём к одинаковым основаниям. Зная, что
. Приведём к одинаковым основаниям. Зная, что 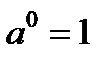 , представим правую часть неравенства, как
, представим правую часть неравенства, как 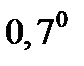 и тогда
и тогда
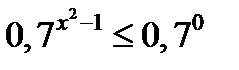
так как 0,7 < 1, то функция убывающая и значит  . Это квадратное неравенство, которое решается методом интервалов.
. Это квадратное неравенство, которое решается методом интервалов.
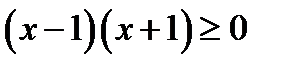
| + |
| – |
| + |
| –1 1 |
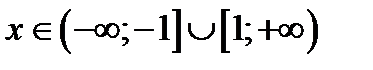
4.2. Метод логарифмирования обеих частей неравенства.
в) 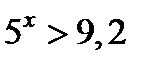
Привести к одинаковым основаниям не представляется возможным. Используем метод логарифмирования.
 , т.к.
, т.к. 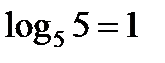 , то
, то
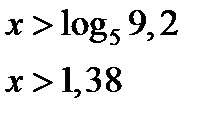
| 1,38 |
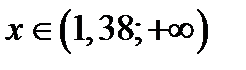
Можно логарифмировать обе части неравенства по любому основанию. Например по основанию 10.
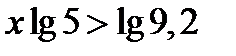
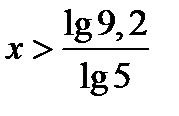 , т.к.
, т.к. 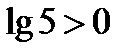 и
и 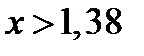 . Ответ тот же.
. Ответ тот же.
г) 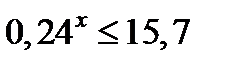 Прологарифмируем по основанию «е»
Прологарифмируем по основанию «е»
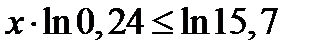 , т.к.
, т.к. 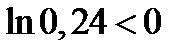 ,
,
то 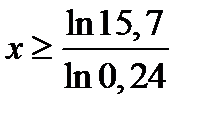
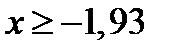
| –1,93 |
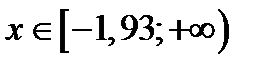
д) 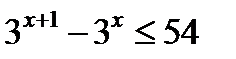 Используя свойство степени, имеем
Используя свойство степени, имеем 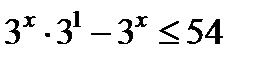 ; вынесем
; вынесем 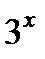 за скобки
за скобки 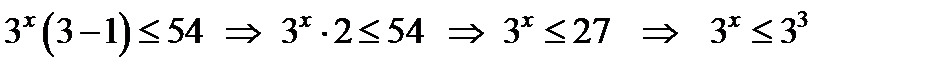 , т.к. 3 > 1, то
, т.к. 3 > 1, то 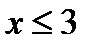
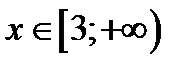
Затем решаются неравенства
Стр. 31 пособие «Сборник мат.» № 2.2; 2.3; 2.9; 2.11; 2.12
2.2 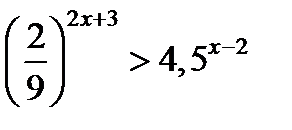 , т.к.
, т.к. 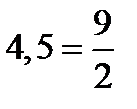 , то
, то 
Учитывая, что 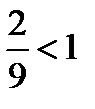 , то
, то
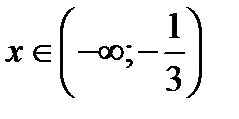
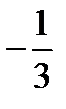
|
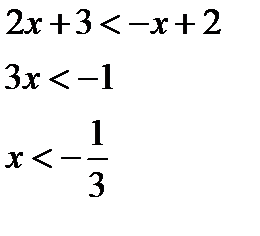
2.3 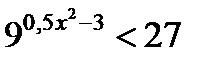 , приведем к основанию 3
, приведем к основанию 3
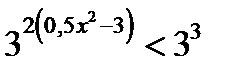 , т.к. 3 > 1, то
, т.к. 3 > 1, то
| + |
| + |
| – |
| –3 |
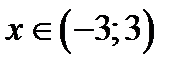
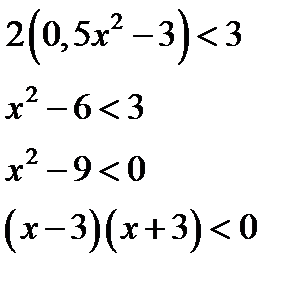
2.9 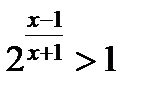
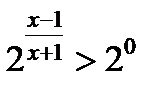 , т.к. 2 > 1, то
, т.к. 2 > 1, то
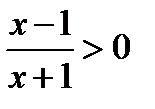
| –1 |
| + |
| + |
| – |
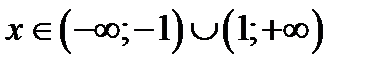
2.11  . В левой части неравенства надо умножить степени с одинаковым показателем. Т.к.
. В левой части неравенства надо умножить степени с одинаковым показателем. Т.к. 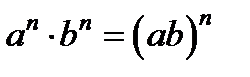 , то
, то 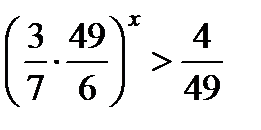 . Сокращаем дроби и получим
. Сокращаем дроби и получим
, т.к. 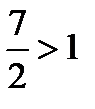 , то , то
|
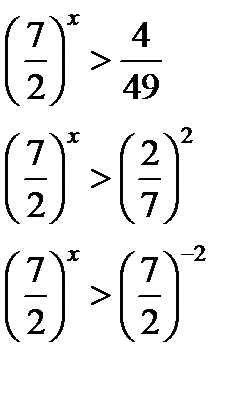
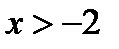
| –2 |
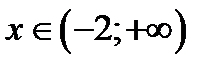
2.12
, т.к.  , то , то
|
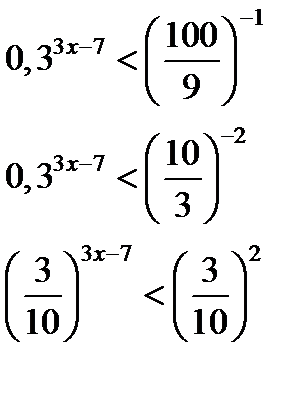
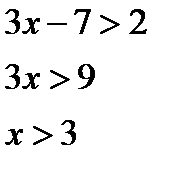
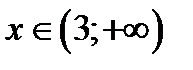
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|