
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Корреляционный момент. Коэффициент корреляции
Корреляционный момент
Определение 2. Корреляционным моментом случайных величин X и Y (или ковариацией) называется математическое ожидание произведений их отклонений:
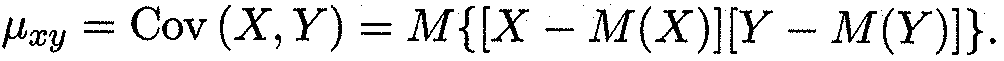
Корреляционный момент служит для описания связи между случайными величинами X и Y. Из свойств математического ожидания легко убедиться в том, что μху можно записать в следующем виде:
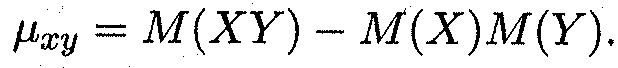 Для непосредственного вычисления корреляционного момента (ковариации) используется формула (см. распределение (15.21))
Для непосредственного вычисления корреляционного момента (ковариации) используется формула (см. распределение (15.21))
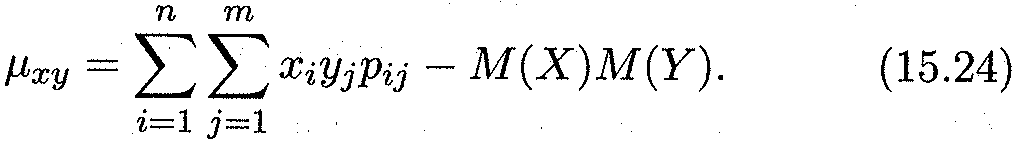
ТЕОРЕМА 15.3. Корреляционный момент двух независимых случайныx величин X и Y равен нулю.
Если корреляционный момент μху не равен нулю, то, стало быть, величины X и Y являются зависимыми.
Коэффициент корреляции
Из определения корреляционного момента следует, что его размерность равна произведению размерностей величин X и Y; например, если X и Y измерены в сантиметрах, то μху имеет размерность см2.
Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Для устранения этого недостатка вводят безразмерную числовую характеристику — коэффициент корреляции, величина которого не зависит от выбора системы измерения случайных величин.
Определение 3. Коэффициентом корреляции случайных величин X и Y называется отношение их корреляционного момента к произведению средних квадратических отклонений этих величин:
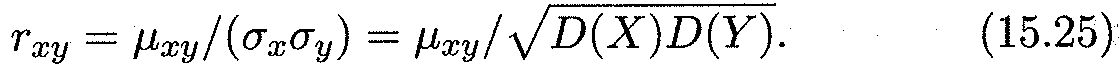 Из определения и свойств математического ожидания и дисперсии следует важный вывод, что абсолютная величина коэффициента корреляции не превосходит единицы:
Из определения и свойств математического ожидания и дисперсии следует важный вывод, что абсолютная величина коэффициента корреляции не превосходит единицы:

Определение 4.Две случайные величины X и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля (т.е. величины зависимы); если же их корреляционный момент равен нулю, то X и У называются некоррелированными.
Таким образом, две коррелированные случайные величины (т.е. при rху ≠ 0) являются также и зависимыми. Обратное утверждение неверно, т.е. две зависимые величины могут быть как коррелированными, так и некоррелированными.
Пример 2. Найти корреляционный момент и коэффициент корреляции двух случайных величин X и У, распределения которых заданы в предыдущем примере 1. 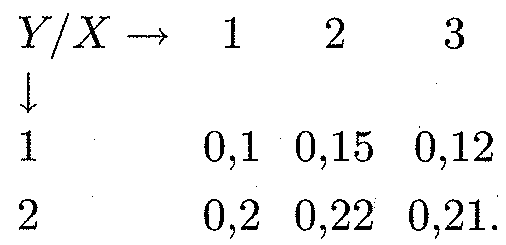
Решение.Воспользуемся формулами (15.24), 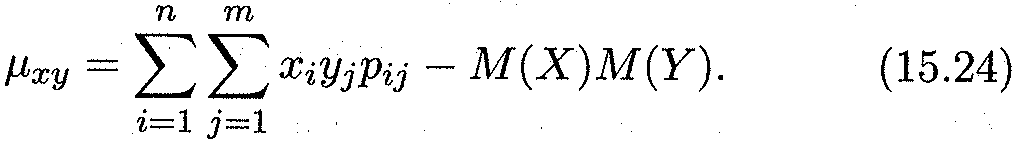
(15.26),
атакже формулой вычисления центрального момента второго порядка (15.19); 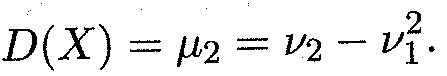
последовательно вычисляем:
М(Х)=0,1+0,2+0,3+0,44+0,36+0,63=2,03, М(У)=0,1+0,15+0,12+0,4+0,44+0,42=1,63,
М(Х2)=0,1+0,2+0,6+0,88+1,08+1,89=4,75
{М(Х)}2 =4,1209,
D(X) = D(X) = М(Х2) - [М(Х)}2=4,75-4,1209=0,629, D(Y) = 0,233,
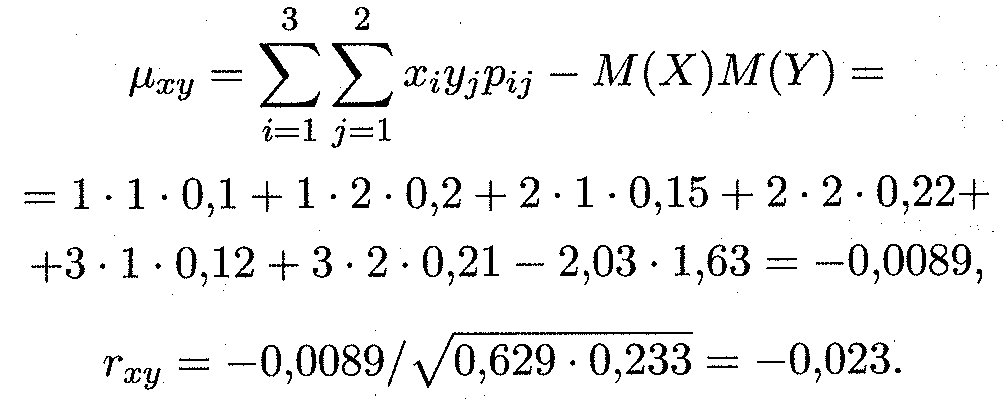
В данном случае коэффициент корреляции близок к нулю; это означает, что случайные величины X и У слабокоррелированы.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|