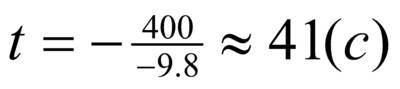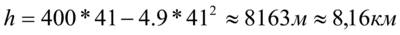Хелпикс

Главная

Контакты

Случайная статья



Если r = n, где n ∈ N, то получим функцию у = , х  (– ; + ).

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


1) Если r = n, где n ∈ N, то получим функцию у = , х  (– ; + ).

На рисунке 1 изображены графики функций у = , где n – четное.

На рисунке 2 изображен график функций у = , где n – нечетное.

2) Если r = − n, где n ∈ N, то получим функцию у = , х  0.

На рисунке 3 изображен график функций у = 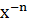, где n – четное.

Рис. 2
у =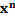
Х
У
Х
У
Рис. 1
у =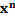
у =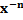
У
X
Рис. 3
Рис. 4
X
у =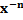
У

На рисунке 4 изображен график функций у = 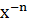, где n – нечетное.

 3) Рассмотрим степенную функцию у = , где r =  (m и n – натуральные числа).

На рисунке 5 изображенграфик функций у = 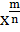,где 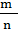 ˃ 1, x ≥ 0.

На рисунке 6 изображен график функции у = 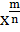, где 0 ˂  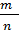˂ 1, х ≥ 0.

Свойства функций у = , где r =  ˃ 0.

1) D(f) = [0; + ∞);

2) функция не является и четной, ни нечетной;

3) возрастает на D(f);

4) ограничена снизу;

5) не имеет наибольшего значения, унаим. = 0;

6) непрерывна;

7) Е(f) = [0; + ∞).

 На рисунке 7 изображен график функцию у = 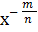 или

 у = 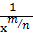, х > 0.

Свойства функций у = 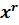, r = − :

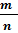1) D(f) = (0; + ∞);

2) функция не является и четной, ни нечетной;

3) убывает на D(f);

4) ограничена снизу;

5) не имеет наибольшего и наименьшего значения;

6) непрерывна;

7) Е(f) = (0; + ∞)

РЕШЕНИЕ ПРИМЕРОВ

Пример 1.

 Найти множество значений функции:

.

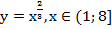Поскольку функция, как нам известно, монотонно возрастает, вычислим значения в граничных точках, и интервал значений между ними и будет искомое множество значений.

.

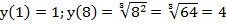Ответ: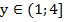

 Задача 2.

Рассмотрим задачу из физики (пример практического применения степенных функций):

На учебном полигоне произведён выстрел из зенитного орудия в вертикальном направлении. Требуется определить наибольшую высоту подъёма снаряда h, время подъёма t1 и время падения t2, если начальная скорость снаряда V0 = 400 м/с. Сопротивлением воздуха пренебречь.

 

Решение:

Вопрос Ответ На доске
Что дано в задаче? Начальная скорость снаряда V0 = 400 м/с, указано направление выстрела. Дано: V0 = 400 м/с.
Что нужно найти? Наибольшую высоту подъёма снаряда, время подъёма и время падения. Найти h, t1,t2.

Записываем решение.

 Решение.
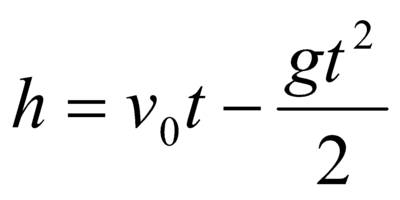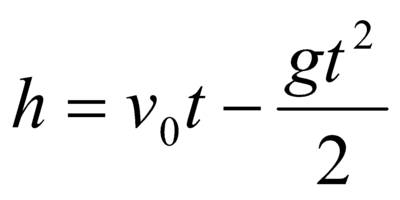Какой функцией выражается закон движения снаряда? Квадратичной функцией , где g – ускорение свободного падения, g = 9.8 м/с. g = 9.8 м/с.
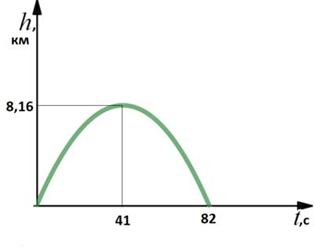
А что будет графиком данной функции? Графиком данной функции является парабола.

Рисунок

 

 
Куда будут направлены её ветви? Ветви параболы направлены вниз.
Где, следовательно, будет наибольшая высота подъёма снаряда? Наибольшая высота подъёма снаряда будет в вершине параболы.
Что необходимо знать для нахождения наибольшей высоты? Необходимо найти координаты вершины параболы.
Что мы получим, подставив данные?

;

Как найти время падения снаряда?

Время подъёма снаряда соответствует интервалу возрастания функции и равно 41с. Время падения снаряды соответствует интервалу убывания функции и равно времени подъёма, так как график функции симметричен относительно прямой, проходящей через вершину параболы.
Ответ:

Ответ: h = 8.16 км; t1 = t2 ≈ 41c.

⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
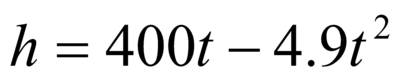
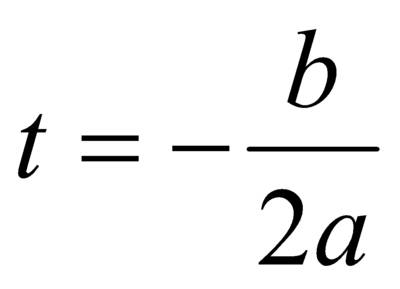