
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Степень с рациональным показателем
Степень
Степенью называется выражение вида: 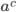 , где:
, где:
§ 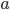 — основание степени;
— основание степени;
§  — показатель степени.
— показатель степени.
Степень с натуральным показателем {1, 2, 3,...}
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
1. По определению: 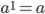 .
.
2. Возвести число в квадрат — значит умножить его само на себя: 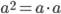
3. Возвести число в куб — значит умножить его само на себя три раза: 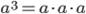 .
.
Возвести число в натуральную степень 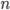 — значит умножить число само на себя
— значит умножить число само на себя 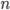 раз:
раз:
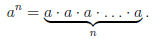
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
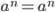 , n > 0
, n > 0
Возведение в нулевую степень:
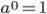 , a ≠ 0
, a ≠ 0
Если показателем степени является целое отрицательное число:
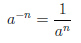 , a ≠ 0
, a ≠ 0
Прим: выражение 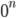 не определено, в случае n ≤ 0. Если n > 0, то
не определено, в случае n ≤ 0. Если n > 0, то 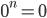
Пример 1.
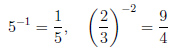
Степень с рациональным показателем
Если:
§ a > 0;
§ n — натуральное число;
§ m — целое число;
Тогда:
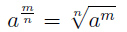
Пример 2.
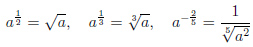
Свойства степеней
| Произведение степеней | 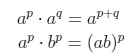
|
| Деление степеней | 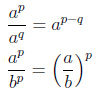
|
| Возведение степени в степень | 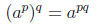
|
Пример 3.
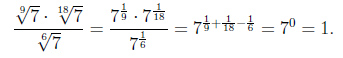
Корень
Арифметический квадратный корень
Уравнение 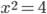 имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
Рассмотрим уравнение 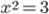 . Нарисуем график функции
. Нарисуем график функции 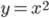 и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
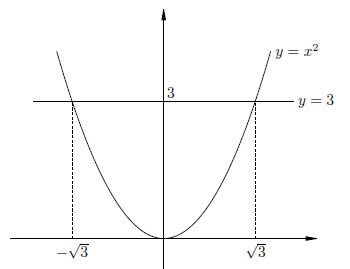
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень 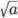 — это неотрицательное число, квадрат которого равен
— это неотрицательное число, квадрат которого равен 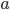 , a ≥ 0. При a < 0 — выражение
, a ≥ 0. При a < 0 — выражение 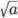 не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу
не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу 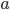 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|