Хелпикс

Главная

Контакты

Случайная статья



Модель системы в пространстве состояний

⇐ ПредыдущаяСтр 2 из 2


Модель системы в пространстве состояний

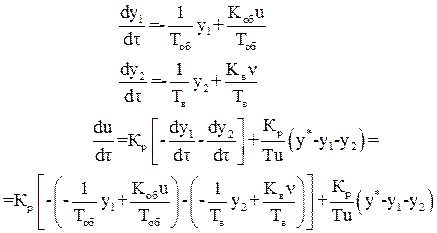
Листинг программы моделирования САР в программе MathCad:

 

 

Графики переходных процессов управления

Для начала проверим работу программы при нулевых значениях yзад и νmax.

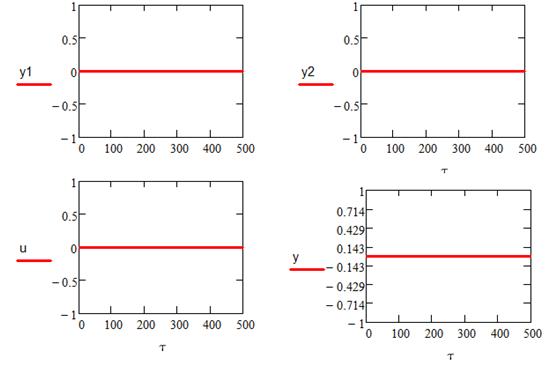
Пусть значение возмущающего воздействия равно ν= νmax/2=0,3/2=0,15, а заданное значение равняется yзад=0

 σ

Система устойчива;

Время регулирования -τр=0 с (т.к. emax=0,01)

Динамическая ошибка- σ=0,0014;

Статическая ошибка- ∆=0.

Пусть значение возмущающего воздействия равно ν= νmax=0,3, а заданное значение равняется  yзад=0

 σ

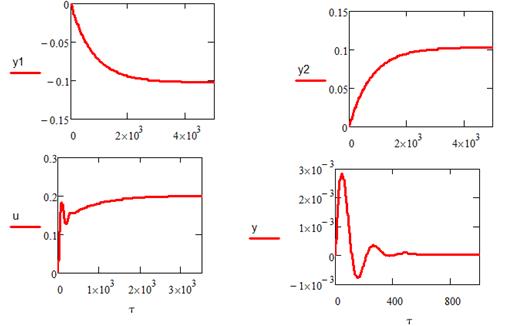
Система устойчива;

Время регулирования -τр=0 с (т.к. emax=0,01);

Динамическая ошибка- σ=0,0028;

Статическая ошибка- ∆=0.

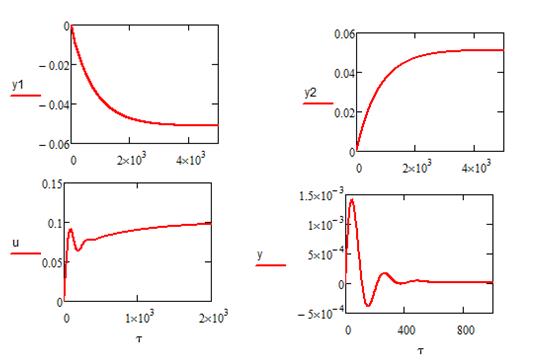
Пусть заданное значение равняется yзад=0,2, возмущение отсутствует ν= 0

 τр
 σ

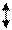
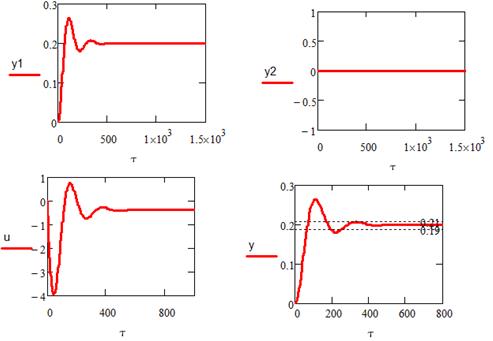
Система устойчива;

Время регулирования -τр=250 с;

Динамическая ошибка- σ=0,06;

Статическая ошибка- ∆=0.

Зададим возмущающее воздействие равное ν=0,2 и изменим значение заданной величины  yзад=0,05

 τр
 σ

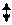
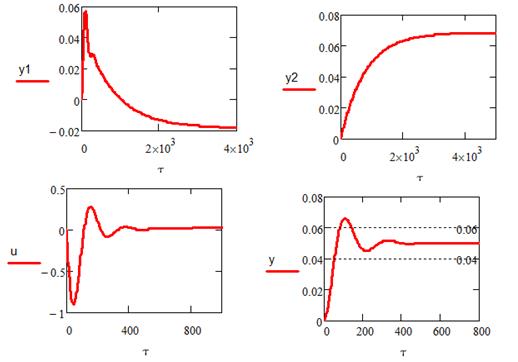
Система устойчива;

Время регулирования -τр=165 с;

Динамическая ошибка- σ=0,015;

Статическая ошибка- ∆=0.

Проверим систему на робастность. Оставим параметры прежние, только увеличим постоянную времени объекта (ν=0,2 и yзад=0,05, Тоб=540 (исходное значение Тоб=490))

 τр
 σ

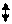
Система устойчива;

Время регулирования -τр=165 с;

Динамическая ошибка- σ=0,015;

Статическая ошибка- ∆=0.

Вывод

В ходе выполнения лабораторной работы были приобретены умения и навыки параметрического синтеза САР промышленных объектов. Так же было проведено исследование работоспособности системы методами математического моделирования.

По результатам исследования системы управления на устойчивость, инвариантность, ковариантность и робастность можно сделать вывод, что одноконтурная система устойчива, так как все переходные процессы имеют затухающий вид, кроме того система инвариантна к возмущениям. Стоит отметить, что изменяя заданное значение, система смогла его отследить, значит, её можно назвать ковариантной с заданием. Кроме того, система прошла проверку на наличие такого свойства, как робастность.

На основании вышесказанного, можно считать данную САР работоспособной.

 


 

Список используемой литературы

1. Алексеев А.А. и др. Теория управления. Учеб./СПб.: Изд-во СПб ГЭТУ «ЛЭТИ». 1999. – 435 с.;

2. Ротач В.Я. Расчет настройки промышленных систем регулирования. М.: Госэнергоиздат, 1961. – 344 с.

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.