Свойства функции при четных n. График и свойства функции

3. Свойства функции при четных n

Вернемся к функции 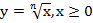. Прочтем ее график и перечислим основные свойства.

1. Если аргумент возрастает от нуля до бесконечности, то функция также возрастает от нуля до бесконечности и проходит через точки (0;0), (1;1) при любом n;

2. Область определения: ;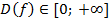

3. Функция общего вида (не является четной либо нечетной);

4. Функция возрастает на луче ;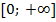

5. Не ограничена сверху, но ограничена снизу;

6. Не имеет наибольшего значения, но имеет наименьшее значение ;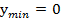

7. Непрерывна;

8. Область значений: ;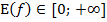

9. Выпукла вверх на луче 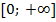. Это означает, что мы можем взять произвольные точки А и В на графике, соединить их отрезком и содержащийся между этими точками кусок графика будет находиться над отрезком;

10. Функция имеет производную при любом х большем нуля; при 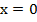функция не имеет производной, касательной в этой точке является ось у.

4. График и свойства функции

Рассмотрим функцию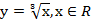

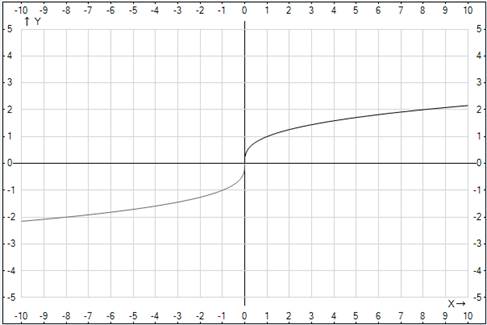
Рис. 5. График функции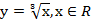

Докажем, что данная функция нечетная:

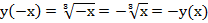
Итак, функция 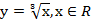нечетная, ее график симметричен относительно начала координат.

График функции проходит через точки (0;0), (1;1), (-1;-1)

Функция касается оси у.

Аналогичными свойствами и особенностями обладают функции 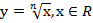при любом нечетном n.

⇐ Предыдущая 123 Следующая ⇒