Функции y=n√x, их свойства и графики

Функции y=n√x, их свойства и графики

Задание построить графики функции y=n√x при четном и нечетном n и описать свойства функции.

На данном уроке мы рассмотрим функцию y=(√x)ⁿ, её основные свойства, и построим графики.

1. Определение корня n-й степени, существование функций вида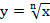

Напомним основное определение.

Определение:

Корнем n-ой степени из неотрицательного числа а при четном n называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.

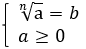
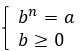
Например: 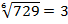, т. к. 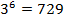; 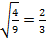, т. к.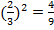

Из определения следует важный вывод:

На множестве значений 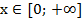существует функция 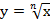при 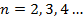, т. е. при любом натуральном n, не равном единице.

Вспомним, что называется функцией.

2. Функция у=х, теорема о симметрии графиков функций

Определение:

Функцией называется закон соответствия, по которому каждому значению аргумента х ставится в соответствие единственное значение функции у.

Рассмотрим исследуемую функцию при :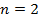

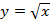
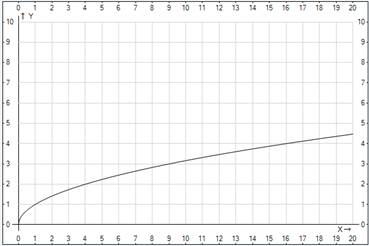
Рис. 1. График функции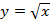

Очевидно, что представленный график (Рис. 1.) проходит через точки (1;1), (4;2), (9;3) и т. д.

Чтобы избавиться от корня, возведем функцию в квадрат, наложив условие на у:

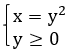
Рассмотрим две функции. Первая – 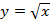при 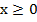, график ее – это часть параболы. Вторая функция – 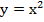при 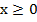, это также часть параболы. Данные ветви парабол симметричны относительно прямой 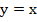. графики имеют две общие точки: (0;0) и (1;1). На ветви параболы 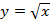лежат точки с координатами 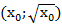, на ветви параболы 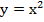– точки с координатами 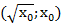. Эти точки симметричны относительно прямой 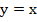. Рис. 2.

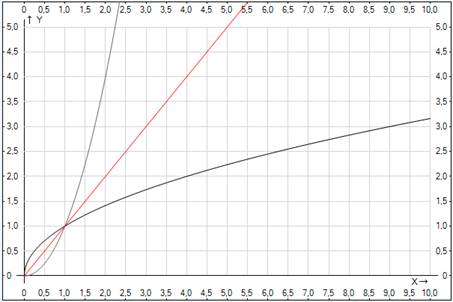
Рис. 2. Графики функци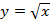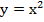й , и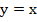

Теорема:

Точки А(а;b) и В(b,a) симметричны относительно прямой .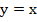

Доказательство:

Рассмотрим чертеж (рисунок 3). Координаты точки А означают, что прямоугольный треугольник 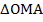имеет катеты а и b. Аналогично треугольник 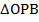имеет те же самые катеты. Таким образом, рассмотренные треугольники равны, и из их равенства следует равенство углов 1 и 2 и равенство гипотенуз ОА и ОВ. Напомним, что прямая 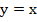является биссектрисой, отсюда углы 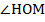и 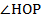составляют по 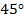, таким образом, углы 3 и 4 равны (т. к. равны углы 1 и 2). Отсюда ОН – биссектриса в равнобедренном треугольнике . Биссектриса, как известно, является осью симметрии для всего треугольника, в том числе и для интересующих нас точек А и В.

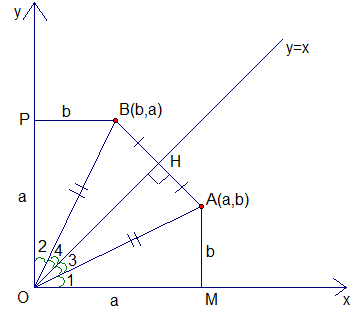
Рис. 3. Чертеж к теореме

Доказанная теорема позволяет сделать вывод для любого n:

График функци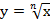и при 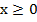симметричен графику функци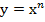и при 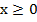относительно прямой .

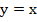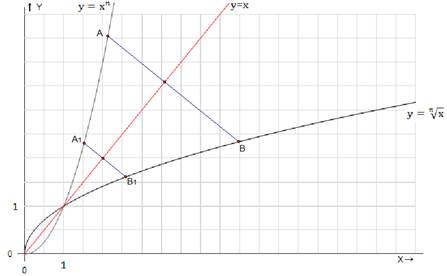
Рис. 4. Обобщение теоремы

12 3 Следующая ⇒