Хелпикс

Главная

Контакты

Случайная статья



Метод Ньютона-Котеса. Метод Гаусса. Пример выполнении лабораторной работы

⇐ ПредыдущаяСтр 2 из 2


Метод Ньютона-Котеса

Основан на замене подынтегральной функции полиномом произвольной степени n. Узлы расположены равномерно на отрезке интегрирования. Квадратурная формула

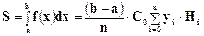, где 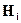-веса, приведенные в табл.1.

                                                                                                                    Таблица 1

n C0 H0 H1 H2 H3 H4 H5 H6
½ - - - - -
1/3 - - - -
3/8 - - -
2/45 - -
5/288 -
1/140

Нетрудно заметить, что при n = 1 и n = 2 формула Ньютона-Котеса полностью соответствует формуле трапеций и формуле Симпсона.

Метод Гаусса

Основан на замене подынтегральной функции полиномом Чебышева. Узлы расположены на отрезке интегрирования неравномерно. Квадратурная формула 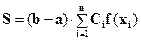, , 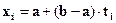где 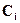 -веса;  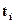-абсциссы; 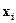- узлы.

 

n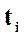
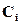
0.2113248654052 0.7886751345948 0.5 0.5
  0.1127016653795 0.5 0.8872983346205 0.2777777777775 0.4444444444449 0.2777777777775
  0.0694318442029 0.3300094782075 0.6699905217925 0.9305681557971 0.1739274225687 0.3260725774312 0.3260725774312 0.1739274225687
    0.0469100770305 0.2307653449475 0.5 0.7692346550525 0.9530899229695 0.118463442528 0.239314335250 0.284444444444 0.239314335250 0.118463442528
    0.0337652428984 0.1693953067669 0.3806904069584 0.6193095930416 0.8306046932331 0.9662347571016 0.0856622461896 0.1803807865241 0.2339569672863 0.2339569672863 0.1803807865241 0.0856622461896

 

Пример выполнении лабораторной работы

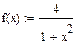         Подынтегральная функция

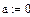
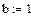            Пределы интегрирования

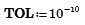  Зададим повышенную точность вычислений

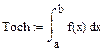
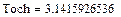               Практически точное значение интеграла

Относительные погрешности при одинаковом числе узлов

Метод прямоугольников

       

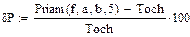
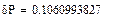
Метод трапеций

       

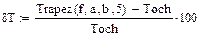
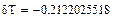
Метод Симпсона

    

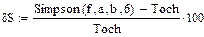
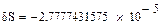
 Метод Ньютона-Котеса

       

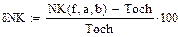
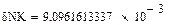
 Метод Гаусса

       

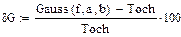
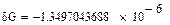
 По точности методы расположились в следующем порядке:

1Метод Гаусса

2Метод Симпсона

3Метод Ньютона-Котеса

4Метод прямоугольников

5Метод трапеций

 

Подпрограмма вычисления интеграла методом прямоугольников

 

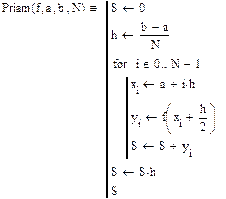
Подпрограмма вычисления интеграла методом трапеций

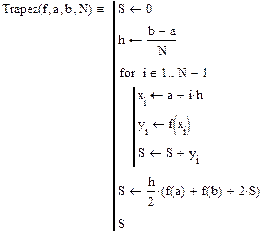
Подпрограмма вычисления интеграла методом Симпсона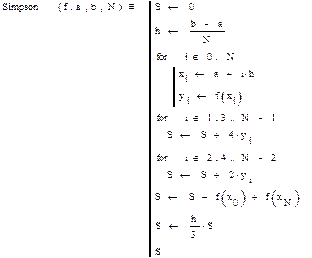

 

Подпрограмма вычисления интеграла методом Ньютона-Котеса для шести узлов

 

 

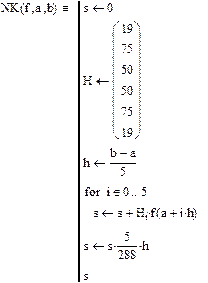
Подпрограмма вычисления интеграла методом Гаусса для шести узлов

 

 

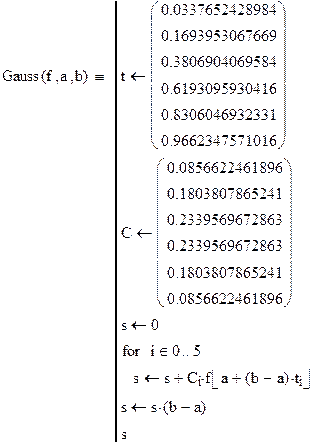
3. Рабочее задание

1. Ознакомиться с методами численного интегрирования;

2. Ввести Mathcad-документ и получить такие же результаты, как в примере;

3. Задать свою подынтегральную функцию и пределы интегрирования согласно таблице вариантов;

4. Вычислить определенный интеграл при n=5, выписав погрешности интегрирования для каждого метода.

5. Расположить методы в порядке убывания точности.

 

 

                                                                                                               Таблица

№ Функция f(x) Отрезок интегрирования № Функция f(x) Отрезок интегрирования
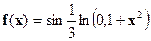
[1;3] 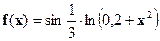[1;3]
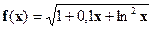
[1;3] 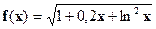[1;3]
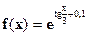
[0;2] 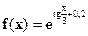[0;2]
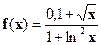
[2;4] 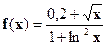[2;4]
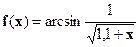
[1;3] 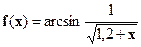[1;3]
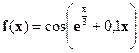
[0;2] 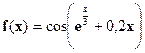[0;2]
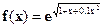
[0;2] 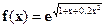[0;2]
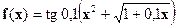
[1;3] 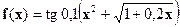[1;3]
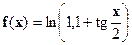
[0;2] 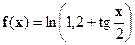[0;2]
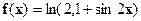
[0;2] 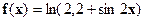[0;2]

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.